Elaborazione dei Segnali

La teoria degli spazi di Hilbert diventa uno strumento potentissimo per rappresentare segnali — audio, immagini, dati temporali, segnali biomedicali — in modo efficiente, analizzarne la struttura, filtrare rumore, comprimerli, estrarre informazioni e risolvere PDE associate alla loro propagazione.
Infatti l’elaborazione dei segnali si fonda sull'idea che ogni segnale può essere visto come un elemento di uno spazio di Hilbert in modo che le basi ortonormali diventano il linguaggio naturale per rappresentarli, analizzarli e manipolarli.
Che poi si tratti della trasformata di Fourier, delle wavelet, della compressione JPEG o del filtraggio digitale, il cuore del metodo è sempre lo stesso: proiettare un segnale su una base ortonormale adatta.

Un segnale continuo \(x(t)\) definito su un intervallo può essere visto come un elemento di uno spazio di Hilbert, tipicamente \(L^2(\mathbb{R})\) per segnali a energia finita, \(L^2([0,T])\) per segnali periodici o limitati nel tempo. Il prodotto interno è: \[ \langle x, y \rangle = \int x(t)\, y^*(t)\, dt. \] Una base ortonormale \(\{\phi_n\}\) permette di scrivere ogni segnale come: \[ x(t) = \sum_{n} c_n \phi_n(t), \qquad c_n = \langle x, \phi_n \rangle. \] Grazie all'ortogonalità i coefficienti non interferiscono tra loro, grazie alla normalizzazione l’energia del segnale si conserva: \[ \|x\|^2 = \sum_n |c_n|^2. \] Grazie alla completezza la base rappresenta tutto lo spazio dei segnali.

La base ortonormale più famosa è legata alla trasformata di Fourier: \[ \phi_\omega(t) = \frac{1}{\sqrt{2\pi}} e^{i\omega t}. \] Queste funzioni sono ortonormali in \(L^2(\mathbb{R})\): \[ \langle \phi_\omega, \phi_{\omega'} \rangle = \delta(\omega - \omega'). \] La trasformata di Fourier di un segnale $x(t)$ è semplicemente la proiezione del segnale su questa base: \[ X(\omega) = \langle x, \phi_\omega \rangle. \] La trasformata di Fourier è (Teorema di Plancherel) un operatore unitario: \[\mathcal F:L^2(\mathbb R)→L^2(\mathbb R),\;\;\;∥x∥^2=∥\mathcal Fx∥^2.\] Si applica all'analisi in frequenza, al filtraggio passa-basso/alto, all'equalizzazione audio, alla compressione, e alla risoluzione di PDE tramite metodi spettrali.

Per segnali digitali, la base ortonormale diventa: \[ \phi_k[n] = \frac{1}{\sqrt{N}} e^{i 2\pi kn/N}. \] La DFT (Discrete Fourier Transform) è la proiezione del segnale su questa base. La FFT è un algoritmo efficiente per calcolare queste proiezioni. Si applica all'analisi spettrale in tempo reale, alla compressione MP3, alla rimozione del rumore, al riconoscimento vocale.

Le wavelet introducono basi ortonormali localizzate nel tempo e nella frequenza: \[ \psi_{j,k}(t) = 2^{j/2} \psi(2^j t - k). \] Queste funzioni formano una base ortonormale di \(L^2(\mathbb{R})\) e sono utili perché catturano dettagli locali, rappresentano discontinuità molto meglio di Fourier, permettono analisi multirisoluzione, con applicazioni nella compressione JPEG2000, nel denoising di segnali biomedicali, nell'analisi di transienti, nel rilevamento di pattern.

Un filtro lineare può essere visto come un operatore che modifica i coefficienti nella base ortonormale. Esempio: \[ x(t) = \sum_n c_n \phi_n(t) \quad \Rightarrow \quad y(t) = \sum_n H_n c_n \phi_n(t), \] dove \(H_n\) è la risposta del filtro nella base scelta. Nel filtraggio in frequenza vengono modificati i coefficienti di Fourier, nel filtraggio wavelet vengono attenuati o amplificati certi livelli di dettaglio.
La compressione si basa sull’idea che molti segnali hanno una rappresentazione sparsa in una base ortonormale. Ad esempio JPEG usa la base DCT (coseni ortonormali), JPEG2000 usa wavelet ortonormali, MP3 usa basi ortonormali adattate alla psicoacustica.
L'dea chiave: \[ x(t) = \sum_n c_n \phi_n(t) \quad \text{ma molti } c_n \text{ sono piccoli}. \] Quindi si possono eliminare senza perdere qualità percepibile.

La compressione JPEG si basa sulla Discrete Cosine Transform (DCT), che usa una base di coseni ortonormali per separare le frequenze dell’immagine e permettere la compressione. \[ \text{DCT}(x,y) = \sum_{u,v} C_{u,v} \cos\left(\frac{(2x+1)u\pi}{16}\right)\cos\left(\frac{(2y+1)v\pi}{16}\right) \] Possiamo visualizzare le funzioni base della DCT 2D. \[ψ_{u,v}(x,y) = C(u)C(v)\cos\left(\frac{(2x+1)u\pi}{16}\right)\cos\left(\frac{(2y+1)v\pi}{16}\right)\] dove

N = 8 basis_functions = np.zeros((N, N, N, N)) for u in range(N): for v in range(N): for x in range(N): for y in range(N): basis_functions[u, v, x, y] = np.cos((2*x+1)*u*np.pi/(2*N)) * \ np.cos((2*y+1)*v*np.pi/(2*N)) fig, axes = plt.subplots(N, N, figsize=(12, 12)) for u in range(N): for v in range(N): ax = axes[u, v] im = ax.imshow(basis_functions[u, v], cmap='RdBu', vmin=-1, vmax=1) ax.axis('off') ax.set_title(f'({u},{v})', fontsize=8) plt.suptitle(f'Funzioni Base della DCT 2D (N={N})', fontsize=16) plt.tight_layout() plt.show()

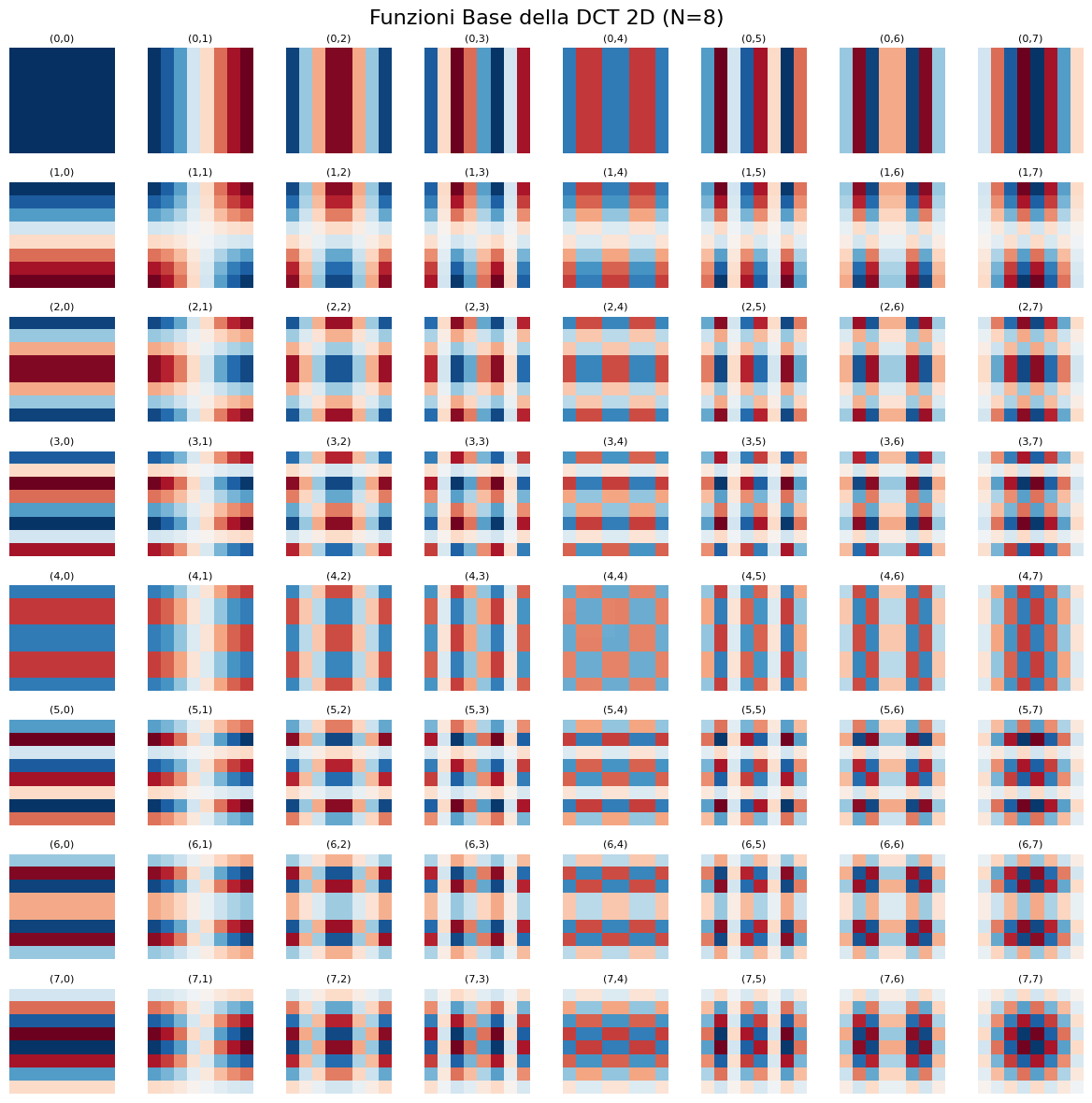
Ad esempio Perciò una parte 8×8 pixel di un'immagine può essere proiettata su questa base.
def DCT2d(block): """ Implementazione manuale della DCT 2D (N=8) """ N = block.shape[0] dct_block = np.zeros((N, N)) # Fattori di normalizzazione C = np.ones(N) C[0] = 1/np.sqrt(2) for u in range(N): for v in range(N): sum_val = 0.0 for x in range(N): for y in range(N): cos_x = np.cos((2*x+1) * u * np.pi / (2*N)) cos_y = np.cos((2*y+1) * v * np.pi / (2*N)) sum_val += block[x, y] * cos_x * cos_y dct_block[u, v] = C[u] * C[v] * sum_val * (2/N) return dct_block def invDCT2d(dct_block): """ Implementazione manuale della DCT 2D inversa """ N = dct_block.shape[0] block = np.zeros((N, N)) # Fattori di normalizzazione C = np.ones(N) C[0] = 1/np.sqrt(2) for x in range(N): for y in range(N): sum_val = 0.0 for u in range(N): for v in range(N): cos_x = np.cos((2*x+1) * u * np.pi / (2*N)) cos_y = np.cos((2*y+1) * v * np.pi / (2*N)) sum_val += C[u] * C[v] * dct_block[u, v] * cos_x * cos_y block[x, y] = sum_val * (2/N) return block
o in modo più efficiente
from scipy.fftpack import dct, idct dct(dct(block.T, norm='ortho').T, norm='ortho') idct(idct(dct_block.T, norm='ortho').T, norm='ortho')
così ad esempio
# blocco 8x8 di esempio (gradiente + un bordo) block = np.array([ [10,12,14,16,18,20,22,24], [10,12,14,16,18,20,22,24], [10,12,14,16,18,20,22,24], [10,12,14,16,18,20,22,24], [200,200,200,200,200,200,200,200], [200,200,200,200,200,200,200,200], [200,200,200,200,200,200,200,200], [200,200,200,200,200,200,200,200], ], dtype=float) C = dct(dct(block.T, norm='ortho').T, norm='ortho') plt.figure(figsize=(10,4)) plt.subplot(1,2,1) plt.imshow(block, cmap='gray') plt.title("Blocco 8×8 originale") plt.colorbar() plt.subplot(1,2,2) plt.imshow(np.abs(C), cmap='hot') plt.title("Modulo dei coefficienti DCT") plt.colorbar() plt.tight_layout() plt.show()

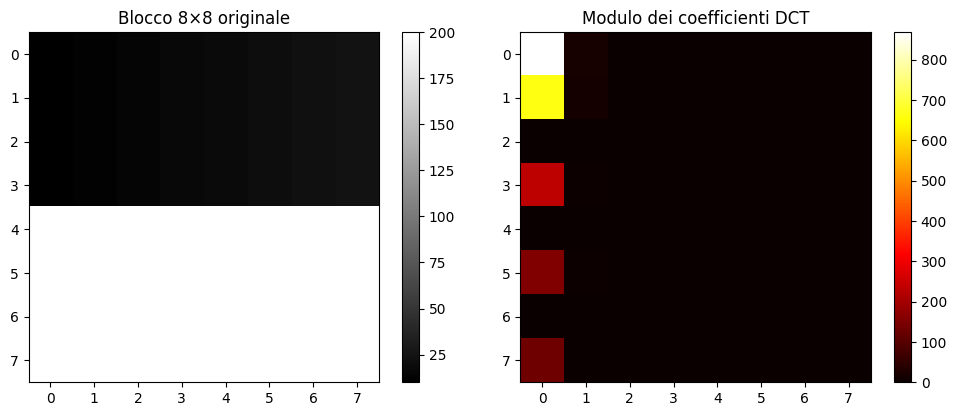
Idea di base della compressione JPEG

Per la compressione MP3 un banco di filtri ortonormale polifase suddivide lo spettro del segnale in 32 bande di frequenza quasi uniformi (bande di Bark) e successivamente la Modified Discrete Cosine Transform (MDCT) determina i coefficienti compressi alla base ortonormale fondamentale.
La MDCT è una variante della DCT-IV, con base formata da funzioni del tipo: \[ \phi_k[n] = w[n] \cos\left[\frac{\pi}{N}\left(n+\frac{1}{2}+\frac{N}{2}\right)\left(k+\frac{1}{2}\right)\right] \] dove \(w[n]\) è una finestra ortonormale adattata alla psicoacustica.

❮❮ ❯❯