Trasformata di Fourier Discreta e Veloce
La trasformata di Fourier discreta (DFT) è uno degli strumenti fondamentali dell’analisi numerica, dell’elaborazione dei segnali e della matematica applicata. Ė un esempio perfetto di come una base ortonormale complessa possa essere utilizzata per cambiare rappresentazione di un vettore.
La DFT è semplicemente la proiezione di un vettore sulle basi ortonormali dei modi complessi, prospettiva geometrica che chiarisce la struttura della trasformata e spiega naturalmente proprietà come invertibilità, conservazione dell’energia e diagonalizzazione delle convoluzioni.
Consideriamo lo spazio vettoriale complesso $\mathbb{C}^{N}=\{\mathbf x:\{0,1,2,\dots,N-1\} \to \mathbb C\}$, di dimensione \(N\), dotato del prodotto scalare standard:
\[
\langle \mathbf x, \mathbf y \rangle = \sum_{n=0}^{N-1} x_n \overline{y_n}.
\]
La DFT non fa altro che cambiare base in questo spazio.
I vettori:
\[
\mathbf v_k = \frac{1}{\sqrt{N}} \left(1, \omega^{-k}, (\omega^2)^{-k}, \dots, (\omega^{N-1})^{-k}\right),
\]
dove
\[
\omega = e^{\frac{2\pi}{N}i}
\]
è la radice \(N\)-esima principale dell’unità, formano una base ortonormale di \( \mathbb{C}^N \),
sono i modi complessi analoghi discreti delle funzioni \( e^{i k x} \) nella trasformata di Fourier continua.
Dato un vettore \(\mathbf x \in \mathbb{C}^N\), la trasformata di Fourier discreta è:
\[\widehat{\mathbf x}=\left(\sum_{n=0}^{N-1} x_n,\sum_{n=0}^{N-1} x_n \, \omega^{-n},\dots,\sum_{n=0}^{N-1} x_n \, \omega^{-kn},\dots, \sum_{n=0}^{N-1} x_n \, \omega^{-(N-1)n} \right)\]
ovvero
\[
\widehat{x}_k = \sqrt{N} \, \langle \mathbf x, \mathbf v_k \rangle = \sum_{n=0}^{N-1} x_n \, \omega^{-nk}.
\]
La DFT fa le proiezioni di \(\mathbf x\) sui vettori della base ortonormale \(\{\mathbf v_k\}.\)
Indichiamo con \(F\) la matrice unitaria (a meno di un fattore \(1/\sqrt{N}\)) i cui vettori riga sono i \(\mathbf v_k\).
import sympy
from sympy import *
π = pi
def DFT_matr(N):
k, n = symbols('k n')
ω = exp(2 * π * I / N)
F = Matrix([[ω**(-k*n) for n in range(N)] for k in range(N)])
return F
N = 8
F = DFT_matr(N)
F
$\left[\begin{matrix}1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\1 & e^{- \frac{i \pi}{4}} & - i & e^{- \frac{3 i \pi}{4}} & -1 & e^{\frac{3 i \pi}{4}} & i & e^{\frac{i \pi}{4}}\\1 & - i & -1 & i & 1 & - i & -1 & i\\1 & e^{- \frac{3 i \pi}{4}} & i & e^{- \frac{i \pi}{4}} & -1 & e^{\frac{i \pi}{4}} & - i & e^{\frac{3 i \pi}{4}}\\1 & -1 & 1 & -1 & 1 & -1 & 1 & -1\\1 & e^{\frac{3 i \pi}{4}} & - i & e^{\frac{i \pi}{4}} & -1 & e^{- \frac{i \pi}{4}} & i & e^{- \frac{3 i \pi}{4}}\\1 & i & -1 & - i & 1 & i & -1 & - i\\1 & e^{\frac{i \pi}{4}} & i & e^{\frac{3 i \pi}{4}} & -1 & e^{- \frac{3 i \pi}{4}} & - i & e^{- \frac{i \pi}{4}}\end{matrix}\right]$
dove
simplify(F * F.H)
$\left[\begin{matrix}8 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 8 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 8 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 8 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 8 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 8 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 8 & 0\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 8\end{matrix}\right]$
In forma matriciale, la sua trasformata di Fourier discreta è:
\[
\widehat{\mathbf x} = F \mathbf x,
\]
Ad esempio.
x = Matrix([sin(2*π*3*n/N) + Rational(1,2)*sin(2*π*7*n/N)
for n in range(N)])
x
$\left[\begin{matrix}0\\\frac{\sqrt{2}}{4}\\- \frac{3}{2}\\\frac{\sqrt{2}}{4}\\0\\- \frac{\sqrt{2}}{4}\\\frac{3}{2}\\- \frac{\sqrt{2}}{4}\end{matrix}\right]$
allora
X = F * x
X
$\left[\begin{matrix}0\\- \frac{\sqrt{2} e^{\frac{i \pi}{4}}}{4} + \frac{\sqrt{2} e^{- \frac{3 i \pi}{4}}}{4} - \frac{\sqrt{2} e^{\frac{3 i \pi}{4}}}{4} + \frac{\sqrt{2} e^{- \frac{i \pi}{4}}}{4} + 3 i\\0\\- 3 i - \frac{\sqrt{2} e^{\frac{i \pi}{4}}}{4} + \frac{\sqrt{2} e^{- \frac{3 i \pi}{4}}}{4} - \frac{\sqrt{2} e^{\frac{3 i \pi}{4}}}{4} + \frac{\sqrt{2} e^{- \frac{i \pi}{4}}}{4}\\0\\- \frac{\sqrt{2} e^{- \frac{i \pi}{4}}}{4} + \frac{\sqrt{2} e^{\frac{3 i \pi}{4}}}{4} - \frac{\sqrt{2} e^{- \frac{3 i \pi}{4}}}{4} + \frac{\sqrt{2} e^{\frac{i \pi}{4}}}{4} + 3 i\\0\\- 3 i - \frac{\sqrt{2} e^{- \frac{i \pi}{4}}}{4} + \frac{\sqrt{2} e^{\frac{3 i \pi}{4}}}{4} - \frac{\sqrt{2} e^{- \frac{3 i \pi}{4}}}{4} + \frac{\sqrt{2} e^{\frac{i \pi}{4}}}{4}\end{matrix}\right]$
o meglio
X = simplify(X)
X
$\left[\begin{matrix}0\\- \frac{\sqrt[4]{-1} \sqrt{2}}{2} - \frac{\left(-1\right)^{\frac{3}{4}} \sqrt{2}}{2} + 3 i\\0\\- 3 i - \frac{\sqrt[4]{-1} \sqrt{2}}{2} - \frac{\left(-1\right)^{\frac{3}{4}} \sqrt{2}}{2}\\0\\\frac{\left(-1\right)^{\frac{3}{4}} \sqrt{2}}{2} + \frac{\sqrt[4]{-1} \sqrt{2}}{2} + 3 i\\0\\- 3 i + \frac{\left(-1\right)^{\frac{3}{4}} \sqrt{2}}{2} + \frac{\sqrt[4]{-1} \sqrt{2}}{2}\end{matrix}\right]$
Graficamente
import matplotlib.pyplot as plt
# Segnale nel dominio del tempo
plt.plot(range(N), x, marker='o')
plt.title("Segnale originale (dominio del tempo)")
plt.xlabel("n")
plt.ylabel("x_n")
plt.show()
# Spettro in modulo
plt.stem([abs(complex(X_k.evalf())) for X_k in X])
plt.title("Modulo della DFT (spettro delle frequenze)")
plt.xlabel("k")
plt.ylabel("|X_k|")
plt.show()
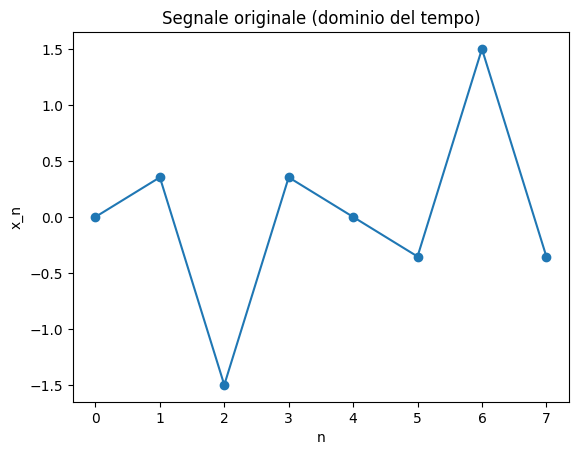
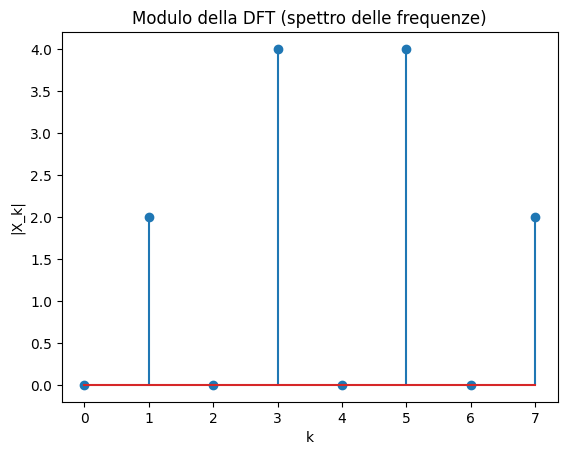
Poiché i \(\mathbf v_k\) formano una base ortonormale, vale la formula di ricostruzione: \[ \mathbf x = \sum_{k=0}^{N-1} \langle \mathbf x, \mathbf v_k \rangle \mathbf v_k. \] Sostituendo: \[ x_n = \frac{1}{N} \sum_{k=0}^{N-1} \widehat{x}_k \, \omega^{nk}, \] che è l'inversa della trasformata di Fourier discreta (IDFT).
Le proprietà che emergono naturalmente dalla visione ortonormale sono
- la matrice \(F\) è unitaria (a fattore \(1/\sqrt{N}\)) perché i vettori \(\mathbf v_k\) sono ortonormali,
- la norma, ovvero l’energia, si conserva sotto un cambio di base ortonormale (Parseval) \[ \sum_{n=0}^{N-1} |x_n|^2 = \frac{1}{N} \sum_{k=0}^{N-1} |\widehat{x}_k|^2, \]
- la convoluzione circolare diventa moltiplicazione punto a punto \[ \widehat{\mathbf x * \mathbf y} = \widehat{\mathbf x} \cdot \widehat{\mathbf y}. \] Infatti se \[ \mathbf x = (x_0, x_1, \dots, x_{N-1}), \qquad \mathbf y = (y_0, y_1, \dots, y_{N-1}) \] la convoluzione circolare \[ (\widehat{\mathbf x * \mathbf y} )_m = \sum_{n=0}^{N-1} \left( \sum_{k=0}^{N-1} x_k\, y_{(n-k)\bmod N} \right) e^{-i\frac{2nm\pi}{N}} \] che scambiando le somme diventa \[ (\widehat{\mathbf x * \mathbf y} )_m = \sum_{k=0}^{N-1} x_k \sum_{n=0}^{N-1} y_{(n-k)\bmod N} e^{-i\frac{2nm\pi}{N}} \] e se poi facciamo il cambio di variabile \(r = n-k\) \[ (\widehat{\mathbf x * \mathbf y} )_m = \sum_{k=0}^{N-1} x_k e^{-i\frac{2km\pi}{N}} \sum_{r=0}^{N-1} y_r e^{-i\frac{2rm\pi}{N}}. \]
La Trasformata di Fourier Veloce (FFT) è solo un algoritmo per calcolare la DFT in modo molto più efficiente. Alla base di elaborazione audio/video, compressione (JPEG, MP3), metodi spettrali per PDE, convoluzioni veloci, analisi di segnali e vibrazioni, usa simmetrie e ricorsione (algoritmo di Cooley–Tukey) per una complessità \(O(N \log N)\) invece di \(O(N²)\).
Come applicazione semplice ma interessante si può vedere come estrarre lo spettro delle frequenze in un segnale, ad esempio un segnale composto da tre sinusoidi e rumore.
# -------------------------
# Costruzione del segnale
# -------------------------
Fs = 1000 # frequenza di campionamento (Hz)
T = 1.0 # durata (secondi)
N = int(Fs * T) # numero di campioni
t = np.linspace(0, T, N, endpoint=False)
# segnale: somma di tre sinusoidi + rumore
f1, f2, f3 = 50, 120, 300
signal = (1.0*np.sin(2*np.pi*f1*t) +
0.5*np.sin(2*np.pi*f2*t) +
0.8*np.sin(2*np.pi*f3*t) +
0.3*np.random.randn(N))
# -------------------------
# FFT (Fast Fourier Transform)
# -------------------------
S = np.fft.fft(signal)
freqs = np.fft.fftfreq(N, 1/Fs)
# prendo solo la parte positiva dello spettro
mask = freqs >= 0
freqs_pos = freqs[mask]
S_pos = np.abs(S[mask])
# -------------------------
# Grafici
# -------------------------
plt.figure(figsize=(12,5))
plt.subplot(1,2,1)
plt.plot(t, signal)
plt.title("Segnale nel dominio del tempo")
plt.xlabel("Tempo (s)")
plt.ylabel("Ampiezza")
plt.grid(True)
plt.subplot(1,2,2)
plt.plot(freqs_pos, S_pos)
plt.title("Spettro ottenuto con FFT")
plt.xlabel("Frequenza (Hz)")
plt.ylabel("Ampiezza")
plt.grid(True)
plt.tight_layout()
plt.show()
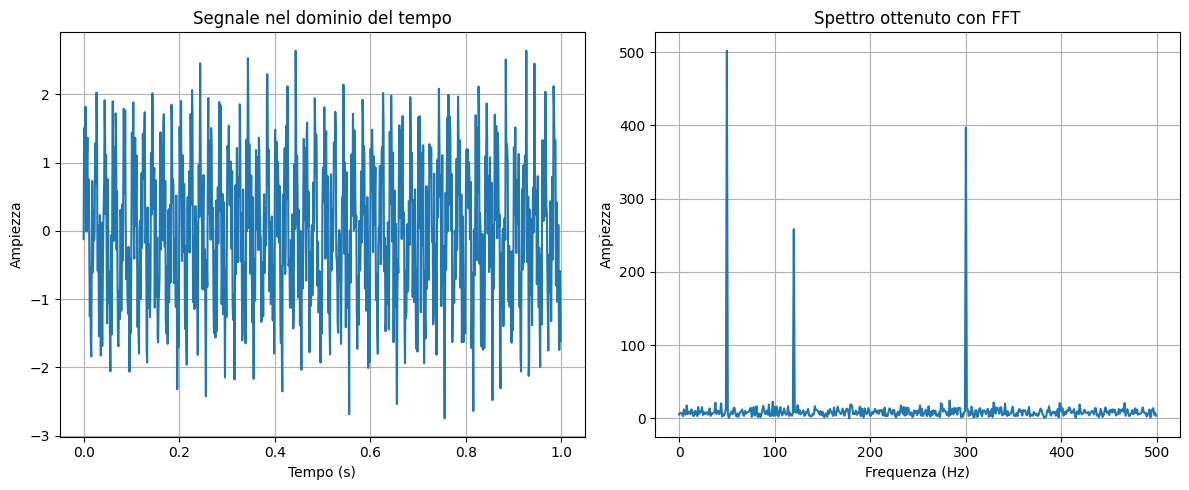
Nel dominio del tempo il segnale sembra caotico mentre nel dominio delle frequenze, la FFT rivela tre picchi netti a: 50 Hz, 120 Hz, 300 Hz, esattamente le frequenze sulla base delle quali era stato costruito.
Si tratta di un esempio di analisi spettrale, alla base del riconoscimento vocale, dell'analisi di vibrazioni meccaniche, della diagnostica medica (ECG, EEG), della spettroscopia e della compressione audio/video