Polinomi di Laguerre
I polinomi di Laguerre, intitolati a Edmond Nicolas Laguerre, sono una sequenza di polinomi ortogonali definiti sull'intervallo \([0,\infty [\), fondamentali in analisi matematica e fisica, specialmente nella meccanica quantistica per risolvere l'equazione di Schrödinger per l'atomo di idrogeno. Sono strettamente correlati ai polinomi generalizzati (o associati) di Laguerre e hanno applicazioni in statistica (distribuzione esponenziale) e metodi numerici, come il metodo iterativo di Laguerre per trovare le radici dei polinomi. Tra le numerose applicazioni si presentano nella trattazione dell'oscillatore armonico quantistico, a causa della loro relazione con i polinomi di Hermite.
Soddisfano l’equazione differenziale \[𝑥𝑦′′+(1−𝑥)𝑦′+𝑛𝑦=0\] e si possono definire \[{\displaystyle L_{n}(x)=\sum_{k=0}^n\frac {(-1)^k}{k!}\binom{n}{k}x^k,\quad \text{per}\quad n=0,1,2,3,\ldots }\] oppure con un'espressione alla Rodrigues \[{\displaystyle L_{n}(x)={\frac {e^{x}}{n!}}{\frac {d^{n}}{dx^{n}}}\left(e^{-x}x^{n}\right),\quad {\text{per}}\quad n=0,1,2,3,\ldots }.\] Sono mutuamente ortogonali rispetto al prodotto interno espresso da \[\displaystyle \langle f,g\rangle =\int _{0}^{\infty }\,f(x)g(x)e^{-x}\,dx.\]
for n in range(7):
print(f"L_{n}(x)=",np.polynomial.laguerre.Laguerre.basis(n).convert(kind=np.polynomial.Polynomial))
L_0(x)= 1.0
L_1(x)= 1.0 - 1.0·x
L_2(x)= 1.0 - 2.0·x + 0.5·x²
L_3(x)= 1.0 - 3.0·x + 1.5·x² - 0.16666667·x³
L_4(x)= 1.0 - 4.0·x + 3.0·x² - 0.66666667·x³ + 0.04166667·x⁴
L_5(x)= 1.0 - 5.0·x + 5.0·x² - 1.66666667·x³ + 0.20833333·x⁴ - 0.00833333·x⁵
L_6(x)= 1.0 - 6.0·x + 7.5·x² - 3.33333333·x³ + 0.625·x⁴ - 0.05·x⁵ + 0.00138889·x⁶
I polinomi generalizzati di Laguerre \(L_n^{(\alpha)}(x)\) sono ortogonali in \(L^2\big([0,\infty[,\, x^\alpha e^{-x}\,dx\big)\) e soddisfano:
\[
\int_0^\infty L_n^{(\alpha)}(x)L_m^{(\alpha)}(x)x^\alpha e^{-x}dx = 0 \quad (n\neq m).
\]
Quindi ogni funzione \(f\) in quello spazio può essere espansa, con la stessa logica che rende fondamentali Fourier, Hermite, Legendre, come:
\[
f(x) = \sum_{n=0}^\infty c_n L_n^{(\alpha)}(x)
\]
I Laguerre sono autofunzioni ortogonali per autovalori reali dell’operatore differenziale autoaggiunto:
\[
\mathcal{L}y = -x y'' - (\alpha+1 - x)y'
\]
con condizioni al contorno appropriate. Permettono una decomposizione spettrale dell’operatore, ciò che in analisi funzionale
è l’analogo infinito-dimensionale della diagonalizzazione di una matrice simmetrica.
Quando il dominio è semi-infinito e la funzione decresce esponenzialmente, i Laguerre sono la base naturale, perfetti per:
- problemi di diffusione su \([0,\infty[\),
- equazioni integrali con kernel esponenziali,
- trasformate di Laplace,
- problemi di probabilità (processi di Poisson, gamma, chi‑quadrato).
In meccanica quantistica, le soluzioni radiali dell’atomo di idrogeno sono: \[ R_{n\ell}(r) \propto r^\ell e^{-r/n} L_{n-\ell-1}^{2\ell+1}(2r/n). \] Infatti l’operatore radiale è un operatore di Sturm–Liouville sul semiasse, e i Laguerre sono la base naturale per diagonalizzarlo.
Sebbene non abbia alcuna relazione con le applicazioni delle basi ortonormali può essere interessante come proprietà strutturali dei polinomi di Laguerre suggeriscano un metodo iterativo per trovare le radici dei polinomi.
Poiché i polinomi di Laguerre \(L_n(x)\) soddisfano l’equazione differenziale
\[
x y'' + (1 - x) y' + n y = 0,
\]
se \(x_k\) è una radice di \(L_n(x)\), allora:
\[
\frac{L_n''(x_k)}{L_n'(x_k)} = \frac{1}{x_k} - \frac{1}{x_k - 1} - \cdots
\]
e soprattutto:
\[
\frac{L_n'(x)}{L_n(x)} = \sum_{k=1}^n \frac{1}{x - x_k}.
\]
Fondamentale che la derivata logaritmica di un polinomio sia la somma dei reciproci delle distanze dalle sue radici*.
Laguerre studiò questa identità per capire come “muoversi” verso una radice.
Per un polinomio generico:
\[
p(z) = a_n \prod_{k=1}^n (z - z_k),
\]
vale sempre:
\[
\frac{p'(z)}{p(z)} = \sum_{k=1}^n \frac{1}{z - z_k}.
\]
E derivando:
\[
\frac{p''(z)}{p(z)} = \left(\frac{p'}{p}\right)^2 - \sum_{k=1}^n \frac{1}{(z - z_k)^2}.
\]
Laguerre osservò che queste identità permettono di costruire un passo iterativo che si avvicina rapidamente a una radice, usando solo \(p, p', p''\).
Laguerre costruì un metodo che “simula” il comportamento di un polinomio con radici tutte reali e distribuite simmetricamente, come i Laguerre stessi.
Il passo iterativo:
\[
z_{k+1} = z_k - \frac{n}{G \pm \sqrt{(n-1)(nH - G^2)}}
\]
dove:
\[
G = \frac{p'(z)}{p(z)}, \qquad
H = G^2 - \frac{p''(z)}{p(z)},
\]
è ottenuto imitando la struttura delle identità dei polinomi di Laguerre.
In particolare \(G\) è la derivata logaritmica, come nei Laguerre, \(H\) è costruito per approssimare la distribuzione delle radici e il denominatore deriva da una stima ottimale della distanza dalla radice più vicina.
Il metodo è quindi una generalizzazione del comportamento dei polinomi di Laguerre applicata a un polinomio qualunque.
I polinomi di Laguerre hanno tre proprietà chiave:
- tutte le radici sono reali e semplici, ciò permette di studiare la dinamica delle radici in modo pulito;
- la derivata logaritmica ha forma particolarmente semplice \[ \frac{L_n'}{L_n} = \sum \frac{1}{x - x_k}; \]
- la loro equazione differenziale fornisce una relazione tra \(p, p', p''\) che Laguerre generalizzò.
# -------------------------
# Metodo di Newton
# -------------------------
def newton_root(p, z0, tol=1e-12, maxiter=50):
z = z0
p1 = np.polyder(p)
history = []
for _ in range(maxiter):
pz = np.polyval(p, z)
history.append(abs(pz))
if abs(pz) < tol:
return z, history
dp = np.polyval(p1, z)
if dp == 0:
return z, history
z = z - pz/dp
return z, history
# -------------------------
# Metodo di Laguerre
# -------------------------
def laguerre_root(p, z0, tol=1e-12, maxiter=50):
n = len(p) - 1
z = z0
p1 = np.polyder(p)
p2 = np.polyder(p, 2)
history = []
for _ in range(maxiter):
pz = np.polyval(p, z)
history.append(abs(pz))
if abs(pz) < tol:
return z, history
dp = np.polyval(p1, z)
ddp = np.polyval(p2, z)
G = dp / pz
H = G*G - ddp/pz
denom1 = G + np.sqrt((n-1)*(n*H - G*G))
denom2 = G - np.sqrt((n-1)*(n*H - G*G))
denom = denom1 if abs(denom1) > abs(denom2) else denom2
z = z - n/denom
return z, history
# -------------------------
# Polinomio di test
# -------------------------
# Un polinomio difficile per Newton: radici multiple e vicine
p = np.poly([1, 1.0001, 2, 3])
z0 = 0.5 + 0.5j # punto iniziale complesso
root_newton, hist_newton = newton_root(p, z0)
root_laguerre, hist_laguerre = laguerre_root(p, z0)
print("Radice trovata da Newton:", root_newton)
print("Radice trovata da Laguerre:", root_laguerre)
# -------------------------
# Grafico dell'errore
# -------------------------
plt.figure(figsize=(8,5))
plt.semilogy(hist_newton, 'o-', label="Newton")
plt.semilogy(hist_laguerre, 's-', label="Laguerre")
plt.xlabel("Iterazione")
plt.ylabel("|p(z_k)| (errore)")
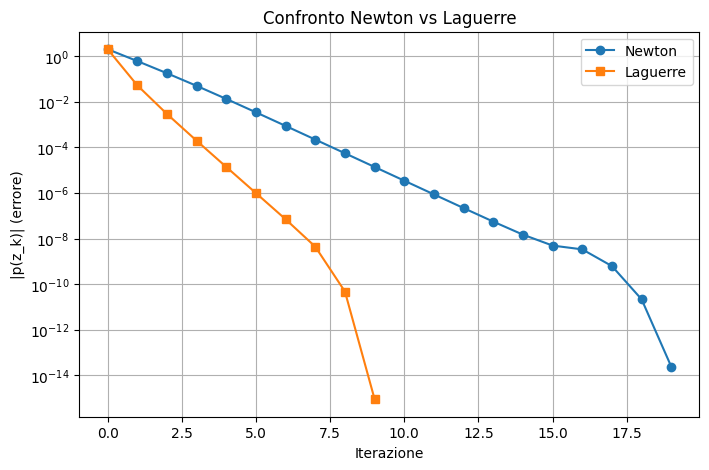
plt.title("Confronto Newton vs Laguerre")
plt.grid(True)
plt.legend()
plt.show()
Radice trovata da Newton: (0.9999999999541085-1.0435238572192822e-10j)
Radice trovata da Laguerre: (1.000000000006048-1.7770049600270808e-13j)