Polinomi di Hermite
Se i polinomi di Legendre e Chebyshev sono confinati in un intervallo limitato, i polinomi di Hermite ci permettono di "mappare" funzioni definite ovunque, a patto che decadano abbastanza velocemente all'infinito. Sono i protagonisti assoluti della Meccanica Quantistica e della Teoria della Probabilità.
Perché una serie di polinomi possa convergere su un intervallo infinito, abbiamo bisogno di una funzione peso estremamente forte che "schiacci" i valori lontano dall'origine, impedendo all'integrale di esplodere.
Per i polinomi di Hermite $H_n$, nella versione "fisica" la funzione peso è la Gaussiana:$$w(x) = e^{-x^2}.$$
Esistono due definizioni standard: quella dei fisici e quella dei probabilisti. In analisi funzionale si usa solitamente quella dei fisici, derivata dalla Formula di Rodrigues:
$$H_n(x) = (-1)^n e^{x^2} \frac{d^n}{dx^n} (e^{-x^2})$$
for n in range(7):
print(f"H_{n}(x)=",np.polynomial.hermite.Hermite.basis(n).convert(kind=np.polynomial.Polynomial))
H_0(x)= 1.0
H_1(x)= 0.0 + 2.0·x
H_2(x)= -2.0 + 0.0·x + 4.0·x²
H_3(x)= 0.0 - 12.0·x + 0.0·x² + 8.0·x³
H_4(x)= 12.0 + 0.0·x - 48.0·x² + 0.0·x³ + 16.0·x⁴
H_5(x)= 0.0 + 120.0·x + 0.0·x² - 160.0·x³ + 0.0·x⁴ + 32.0·x⁵
H_6(x)= -120.0 + 0.0·x + 720.0·x² + 0.0·x³ - 480.0·x⁴ + 0.0·x⁵ + 64.0·x⁶
Se abbiamo una funzione $f(x)$, possiamo scriverla come:$$f(x) = \sum_{n=0}^{\infty} c_n H_n(x).$$ I coefficienti $c_n$ si ottengono proiettando $f(x)$ sui polinomi di Hermite:$$c_n = \frac{1}{\sqrt{\pi} 2^n n!} \int_{-\infty}^{+\infty} f(x) H_n(x) e^{-x^2} dx$$ Ad esempio, volendo analizzare un segnale che ha la forma di un impulso, un pacchetto d'onda, invece di usare infinite onde sinusoidali secondo Fourier si possono usare i polinomi di Hermite. Poiché la base di Hermite "contiene" già il decadimento gaussiano, basteranno pochissimi termini per descrivere l'impulso con estrema precisione.
Ad esempio se consideriamo la funzione esponenziale $$e^x = \sum_{n=0}^{\infty} c_n H_n(x)$$ dove $$c_n = \frac{1}{\sqrt{\pi} 2^n n!} \int_{-\infty}^{+\infty} e^x H_n(x) e^{-x^2} dx.$$ Completando il quadrato all'esponente: $-x^2 + x = -(x - 1/2)^2 + 1/4$, $$c_n = \frac{e^{1/4} }{\sqrt{\pi} 2^n n!}\int_{-\infty}^{+\infty} H_n(x) e^{-(x - 1/2)^2} dx.$$ Usando le proprietà dei polinomi di Hermite (o la loro funzione generatrice), si dimostra l'integrale ha una soluzione molto elegante: $$c_n =\frac{e^{1/4} }{\sqrt{\pi} 2^n n!} \sqrt{\pi} \left( 2 \cdot \frac{1}{2} \right)^n = \frac{e^{1/4} }{\sqrt{\pi} 2^n n!} \sqrt{\pi}= \frac{e^{1/4}}{2^n n!}$$ L'espansione finale in serie di Hermite è dunque:$$e^x = e^{1/4} \left( H_0(x) + \frac{1}{2} H_1(x) + \frac{1}{8} H_2(x) + \frac{1}{48} H_3(x) + \dots \right).$$ Se sostituiamo i polinomi $H_0=1, H_1=2x, H_2=4x^2-2$ otteniamo un'approssimazione che "somiglia" a Taylor ma è bilanciata per minimizzare l'errore dove la gaussiana è più forte (vicino allo zero) \[e^x \approx e^{1/4} \left( \frac{3}{4} + x + \frac{1}{2}x^2\right).\]
def sviluppa_serie(funzione_str, ordine):
"""
funzione_str: stringa della funzione (es. 'sin(x)')
ordine: grado del polinomio
"""
# --- 1. Serie di Taylor (Simbolica - centrata in 0) ---
x = Symbol('x')
f_sym = sympify(funzione_str)
# .series() calcola l'espansione, .removeO() toglie il resto O(x^n)
taylor = f_sym.series(x, 0, ordine + 1).removeO()
# --- 2. Serie di Chebyshev (Numerica - approssimazione in [-1,1]) ---
# Convertiamo la stringa in una funzione Python utilizzabile da NumPy
f_num = lambdify(x, f_sym, 'numpy')
# Interpoliamo sui nodi di Chebyshev (equivalente al troncamento della serie)
chebyshev = cheb.Chebyshev.interpolate(f_num, deg=ordine, domain=[-L, L])
# 3. Hermite (Numerico - Nodi basati sulle radici di Hermite)
# I nodi originali sono distribuiti attorno allo zero.
# Per scalarli su un intervallo specifico [-L, L], usiamo un fattore.
punti_std, pesi = np.polynomial.hermite.hermgauss(ordine + 1)
# Riscaliamo i nodi: il nodo più grande deve corrispondere a L
scala = L / np.max(punti_std)
punti_scalati = punti_std * scala
valori_hermite = f_num(punti_scalati)
hermite = Hermite.fit(punti_scalati, valori_hermite, deg=ordine)
return f_sym, taylor, chebyshev, hermite
# --- Esempio di utilizzo ---
_, t_poly, c_poly, h_poly = sviluppa_serie('exp(x)', 4)
print(f"Taylor (Simbolico): {t_poly}")
print(f"Chebyshev (Coeff.): {c_poly.coef}") # Stampa i coefficienti c0, c1...
print(f"Chebyshev (Polin.):\n{c_poly}") # Rappresentazione T_n(x)
print(f"Hermite (Coeff.): {h_poly.coef}") # Stampa i coefficienti c0, c1...
print(f"Hermite (Polin.):\n{h_poly}") # Rappresentazione H_n(x)
Taylor (Simbolico): x**4/24 + x**3/6 + x**2/2 + x + 1
Chebyshev (Coeff.): [11.30111437 19.51460718 12.82473571 6.59188814 2.52362133]
Chebyshev (Polin.):
11.30111437 + 19.51460718·T₁((0.25x)) + 12.82473571·T₂((0.25x)) +
6.59188814·T₃((0.25x)) + 2.52362133·T₄((0.25x))
Hermite (Coeff.): [19.18700097 20.23226571 16.64282731 3.29365356 1.25822114]
Hermite (Polin.):
19.18700097 + 20.23226571·H₁((0.25x)) + 16.64282731·H₂((0.25x)) +
3.29365356·H₃((0.25x)) + 1.25822114·H₄((0.25x))
def visualizza_grafico(func_str, ordine):
# Calcolo
f_sym, taylor_sym, cheb_poly, herm_poly = sviluppa_serie(func_str, ordine)
# Preparazione dati per il grafico (intervallo leggermente più ampio di [-1, 1])
x_max = 4
x_vals = np.linspace(-x_max, x_max, 500)
x = Symbol('x')
# Conversione in funzioni numeriche per il plot
f_func = lambdify(x, f_sym, 'numpy')
t_func = lambdify(x, taylor_sym, 'numpy')
# Valutazione
y_true = f_func(x_vals)
y_taylor = t_func(x_vals)
y_cheb = cheb_poly(x_vals) # L'oggetto Chebyshev è già chiamabile
y_herm = herm_poly(x_vals)
# --- PLOT ---
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8))
# Grafico 1: Le Funzioni
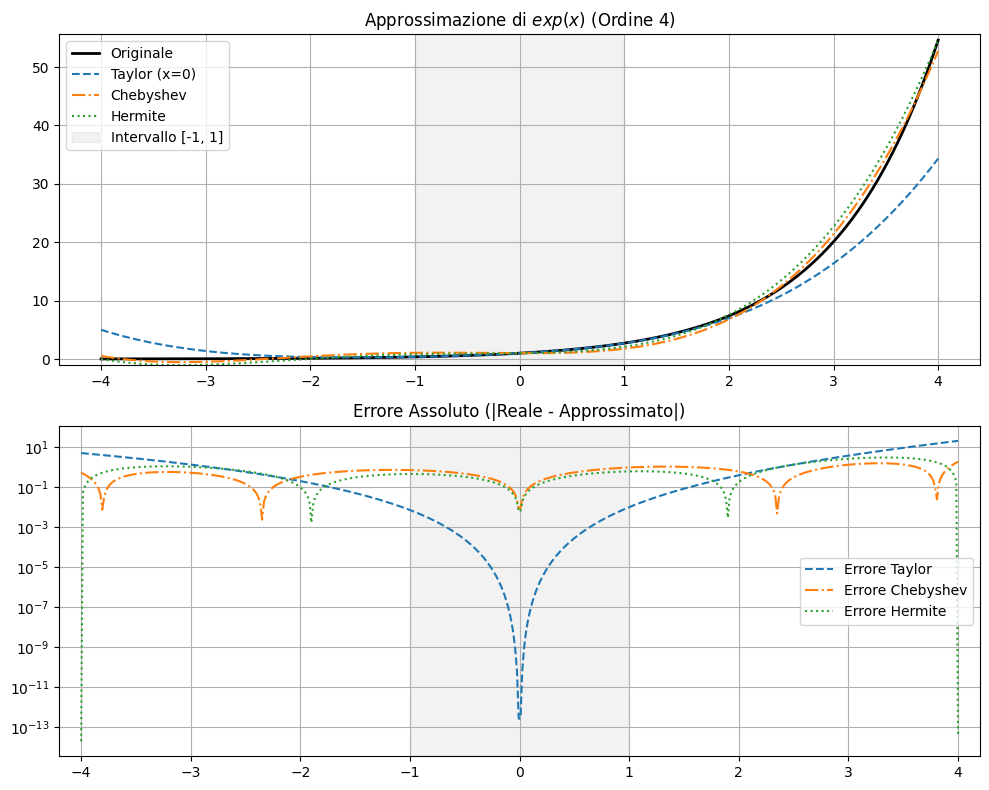
ax1.set_title(f'Approssimazione di ${func_str}$ (Ordine {ordine})')
ax1.plot(x_vals, y_true, 'k-', lw=2, label='Originale')
ax1.plot(x_vals, y_taylor, '--', label='Taylor (x=0)')
ax1.plot(x_vals, y_cheb, '-.', label='Chebyshev')
ax1.plot(x_vals, y_herm, ':', label='Hermite')
ax1.axvspan(-1, 1, color='gray', alpha=0.1, label='Intervallo [-1, 1]')
ax1.set_ylim(min(y_true)-1, max(y_true)+1) # Limita lo zoom verticale
ax1.legend()
ax1.grid(True)
# Grafico 2: L'Errore Assoluto
ax2.set_title('Errore Assoluto (|Reale - Approssimato|)')
ax2.plot(x_vals, np.abs(y_true - y_taylor), '--', label='Errore Taylor')
ax2.plot(x_vals, np.abs(y_true - y_cheb), '-.', label='Errore Chebyshev')
ax2.plot(x_vals, np.abs(y_true - y_herm), ':', label='Errore Hermite')
# Evidenzia la zona di Chebyshev
ax2.axvspan(-1, 1, color='gray', alpha=0.1)
ax2.set_yscale('log') # Scala logaritmica per vedere meglio le differenze
ax2.set_xlim(-x_max-.2, x_max+.2)
ax2.legend()
ax2.grid(True, which="both", ls="-")
plt.tight_layout()
plt.show()
# --- Esegui ---
# Prova con funzioni "difficili" come 1/(1+25*x**2) per vedere il fenomeno di Runge
visualizza_grafico('exp(x)', 4)
La distinzione tra la definizione "fisica" e quella "probabilistica" dei polinomi di Hermite è fondamentale per evitare errori di calcolo, poiché cambiano sia la funzione peso che la normalizzazione.
Mentre i fisici usano la base adatta all'oscillatore armonico, i probabilisti usano una base legata alla distribuzione normale standard $Z \sim \mathcal{N}(0, 1)$
I polinomi di Hermite probabilistici, indicati con $He_n(x)$, sono definiti su tutto $\mathbb R$ con la funzione peso data dalla densità di probabilità gaussiana standard:$$w(x) = \phi(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}$$ La Formula di Rodrigues per questa versione è:$$He_n(x) = (-1)^n e^{\frac{x^2}{2}} \frac{d^n}{dx^n} \left( e^{-\frac{x^2}{2}} \right)$$2.
La relazione tra le due definizioni è quella di una riscalatura delle variabili: $$He_n(x) = 2^{-\frac{n}{2}} H_n\left( \frac{x}{\sqrt{2}} \right)\quad\quad H_n(x) = 2^{\frac{n}{2}} He_n(\sqrt{2}x)$$ I probabilisti preferiscono $He_n$ perchè sono monici, cioè il coefficiente del termine di grado massimo è sempre $1$. Ad esempio: \[\begin{matrix} He_0(x) = 1\\He_1(x) = x\\He_2(x) = x^2 - 1\\He_3(x) = x^3 - 3x\end{matrix}\] La relazione di ortogonalità in ambito probabilistico è molto più "pulita":$$\mathbb{E}[He_n(Z) He_m(Z)] = \int_{-\infty}^{+\infty} He_n(x) He_m(x) \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} dx = n! \delta_{nm}$$In pratica, se prendi una variabile aleatoria normale standard $Z$:La media di ogni polinomio (tranne $He_0$) è zero.La varianza di $He_n(Z)$ è semplicemente $n!$.
- Espansioni di Edgeworth
In statistica, quando una distribuzione non è perfettamente normale, la si può approssimare usando la densità normale moltiplicata per una serie di polinomi $He_n$. Questo permette di correggere l'approssimazione del Teorema del Limite Centrale tenendo conto di asimmetria (skewness) e curtosi. - Il Teorema di Cameron-Martin e il Caos di Wiener
Questa è l'applicazione più avanzata. Nello studio dei processi stocastici (come il Moto Browniano), i polinomi di Hermite probabilistici formano una base ortogonale per lo spazio di Hilbert dei funzionali del processo. Questa struttura è nota come "Scomposizione in Caos di Wiener" ed è lo strumento principale per il calcolo stocastico avanzato (Calcolo di Malliavin). - Prodotti di Wick
In combinatoria e teoria dei campi, i polinomi $He_n(x)$ rappresentano i cosiddetti "prodotti di Wick" di una variabile gaussiana, un modo per gestire le potenze di variabili aleatorie eliminando le correlazioni interne (ortogonalizzazione).
Riassunto delle differenze
| Proprietà | Versione Fisica $H_n$ | Versione Probabilistica $He_n$ |
| Peso | $e^{-x^2}$ | $\frac{1}{\sqrt{2\pi}} e^{-x^2/2}$ |
| Esponente | $-x^2$ | $-x^2/2$ |
| Coefficiente leader | $2^n$ | $1$ (Monico) |
| Normalizzazione | $\sqrt{\pi} 2^n n!$ | $n!$ |