Polinomi di Chebyshev
I polinomi di Chebyshev, intitolati a Pafnutij L'vovič Čebyšëv che li studiò come soluzioni polinomiali dell'equazione differenziale ${\displaystyle (1-x^{2})y''-xy'+n^{2}y=0,}$ sono una sequenza di polinomi ortogonali che giocano un ruolo fondamentale nell'analisi numerica e nella teoria dell'approssimazione.
Se i polinomi di Legendre sono i preferiti dai fisici per studiare la simmetria sferica, i polinomi di Chebyshev sono i preferiti dai programmatori e dai matematici computazionali, perché sono i "campioni" nel minimizzare l'errore di approssimazione.
Esistono due tipi di polinomi di Chebyshev, ma quelli di prima specie sono i più utilizzati.
- I polinomi $T_n$ di Prima Specie nella definizione più elegante, di tipo trigonometrico:$$T_n(x) = \cos(n \arccos x) \quad \text{per } x \in [-1, 1].$$
Sono semplicemente delle onde cosinusoidali "proiettate" sull'asse delle ascisse.
for n in range(7): print(f"T_{n}(x)=",np.polynomial.chebyshev.Chebyshev.basis(n).convert(kind=np.polynomial.Polynomial))T_0(x)= 1.0 T_1(x)= 0.0 + 1.0·x T_2(x)= -1.0 + 0.0·x + 2.0·x² T_3(x)= 0.0 - 3.0·x + 0.0·x² + 4.0·x³ T_4(x)= 1.0 + 0.0·x - 8.0·x² + 0.0·x³ + 8.0·x⁴ T_5(x)= 0.0 + 5.0·x + 0.0·x² - 20.0·x³ + 0.0·x⁴ + 16.0·x⁵ T_6(x)= -1.0 + 0.0·x + 18.0·x² + 0.0·x³ - 48.0·x⁴ + 0.0·x⁵ + 32.0·x⁶Alternativamente possono essere definiti tramite la relazione di ricorrenza: \[\begin{matrix}T_{0}(x)=1 \\T_{1}(x)=x \\T_{n+1}(x)=2xT_{n}(x)-T_{n-1}(x). \end{matrix}\]
- I polinomi $U_n$ di Seconda Specie sono definiti in modo simile:$$U_n(\cos \theta) = \frac{\sin((n+1)\theta)}{\sin \theta}.$$ Questi appaiono spesso in problemi di meccanica dei continui e nello studio di matrici specifiche.
I polinomi $T_n(x)$ formano una base ortogonale nell'intervallo $[-1, 1]$ rispetto a una funzione peso molto particolare:$$w(x) = \frac{1}{\sqrt{1-x^2}}.$$ Quindi:$$\langle T_n, T_m \rangle = \int_{-1}^1 T_n(x) T_m(x) \frac{1}{\sqrt{1-x^2}} dx = 0 \quad (n \neq m).$$ Poiché $w(x)$ tende a infinito quando $x$ si avvicina ai bordi $-1$ e $1$, significa che lo spazio di Hilbert di Chebyshev dà un "peso" enorme a ciò che accade vicino agli estremi dell'intervallo. È proprio questa caratteristica a renderli così efficaci.
Ad esempio possiamo calcolare i coefficienti della serie di Chebyshev per la funzione esponenziale $f(x) = e^x$ nell'intervallo $x \in [-1, 1]$.
Questa scelta è ideale perché la funzione non è periodica (quindi la serie di Fourier standard non sarebbe efficiente) e ci permette di confrontare la precisione di Chebyshev con la celebre serie di Taylor.
Una funzione $f(x)$ può essere espansa in serie di Chebyshev come:$$f(x) = \frac{c_0}{2} + \sum_{n=1}^{\infty} c_n T_n(x)$$I coefficienti $c_n$ si ottengono proiettando la funzione sulla base ortogonale $\{T_n\}$ usando il prodotto interno pesato:$$c_n = \frac{2}{\pi} \int_{-1}^{1} \frac{e^x T_n(x)}{\sqrt{1-x^2}} dx$$
Il calcolo diretto di questo integrale è difficile. Tuttavia, ricordando la definizione $T_n(x) = \cos(n \arccos x)$, possiamo applicare la sostituzione $x = \cos \theta$ (quindi $dx = -\sin \theta d\theta$). L'integrale diventa molto più "familiare":$$c_n = \frac{2}{\pi} \int_{0}^{\pi} e^{\cos \theta} \cos(n\theta) d\theta$$ nell'intervallo $[0, \pi]$ usando $x = \cos(\theta)$.
L'integrale risultante è una forma nota in analisi complessa e funzioni speciali: esso definisce le Funzioni di Bessel modificate di prima specie, indicate con $I_n(z)$. Nello specifico:$$c_n = 2 I_n(1)$$
Per i primi tre termini:
- $c_0$ rappresenta il valore medio "pesato" della funzione.$$c_0 = 2 I_0(1) \approx 2 \times 1.2660 = \mathbf{2.5321}$$
- $c_1$ indica quanta parte della funzione "assomiglia" a una retta ($T_1(x)=x$).$$c_1 = 2 I_1(1) \approx 2 \times 0.5651 = \mathbf{1.1303}$$
- $c_2$ indica la componente parabolica ($T_2(x)=2x^2-1$).$$c_2 = 2 I_2(1) \approx 2 \times 0.1357 = \mathbf{0.2714}$$
def sviluppa_serie(funzione_str, ordine):
"""
funzione_str: stringa della funzione (es. 'sin(x)')
ordine: grado del polinomio
"""
# --- 1. Serie di Taylor (Simbolica - centrata in 0) ---
x = Symbol('x')
f_sym = sympify(funzione_str)
# .series() calcola l'espansione, .removeO() toglie il resto O(x^n)
taylor = f_sym.series(x, 0, ordine + 1).removeO()
# --- 2. Serie di Chebyshev (Numerica - approssimazione in [-1,1]) ---
# Convertiamo la stringa in una funzione Python utilizzabile da NumPy
f_num = lambdify(x, f_sym, 'numpy')
# Interpoliamo sui nodi di Chebyshev (equivalente al troncamento della serie)
chebyshev = cheb.Chebyshev.interpolate(f_num, deg=ordine)
return f_sym, taylor, chebyshev
# --- Esempio di utilizzo ---
_, t_poly, c_poly = sviluppa_serie('exp(x)', 4)
print(f"Taylor (Simbolico): {t_poly}")
print(f"Chebyshev (Coeff.): {c_poly.coef}") # Stampa i coefficienti c0, c1...
print(f"Chebyshev (Polin.):\n{c_poly}") # Rappresentazione T_n(x)
Taylor (Simbolico): x**4/24 + x**3/6 + x**2/2 + x + 1
Chebyshev (Coeff.): [1.26606588 1.1303182 0.27149514 0.04433365 0.00542926]
Chebyshev (Polin.):
1.26606588 + 1.1303182·T₁(x) + 0.27149514·T₂(x) + 0.04433365·T₃(x) +
0.00542926·T₄(x)
def visualizza_grafico(func_str, ordine):
# Calcolo
f_sym, taylor_sym, cheb_poly = sviluppa_serie(func_str, ordine)
# Preparazione dati per il grafico (intervallo leggermente più ampio di [-1, 1])
x_vals = np.linspace(-1.5, 1.5, 500)
x = Symbol('x')
# Conversione in funzioni numeriche per il plot
f_func = lambdify(x, f_sym, 'numpy')
t_func = lambdify(x, taylor_sym, 'numpy')
# Valutazione
y_true = f_func(x_vals)
y_taylor = t_func(x_vals)
y_cheb = cheb_poly(x_vals) # L'oggetto Chebyshev è già chiamabile
# --- PLOT ---
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8))
# Grafico 1: Le Funzioni
ax1.set_title(f'Approssimazione di ${func_str}$ (Ordine {ordine})')
ax1.plot(x_vals, y_true, 'k-', lw=2, label='Originale')
ax1.plot(x_vals, y_taylor, 'r--', label='Taylor (x=0)')
ax1.plot(x_vals, y_cheb, 'b-.', label='Chebyshev')
ax1.axvspan(-1, 1, color='green', alpha=0.1, label='Intervallo [-1, 1]')
ax1.set_ylim(min(y_true)-1, max(y_true)+1) # Limita lo zoom verticale
ax1.legend()
ax1.grid(True)
# Grafico 2: L'Errore Assoluto
ax2.set_title('Errore Assoluto (|Reale - Approssimato|)')
ax2.plot(x_vals, np.abs(y_true - y_taylor), 'r--', label='Errore Taylor')
ax2.plot(x_vals, np.abs(y_true - y_cheb), 'b-.', label='Errore Chebyshev')
# Evidenzia la zona di Chebyshev
ax2.axvspan(-1, 1, color='green', alpha=0.1)
ax2.set_yscale('log') # Scala logaritmica per vedere meglio le differenze
ax2.set_xlim(-1.2, 1.2)
ax2.legend()
ax2.grid(True, which="both", ls="-")
plt.tight_layout()
plt.show()
# --- Esegui ---
# Prova con funzioni "difficili" come 1/(1+25*x**2) per vedere il fenomeno di Runge
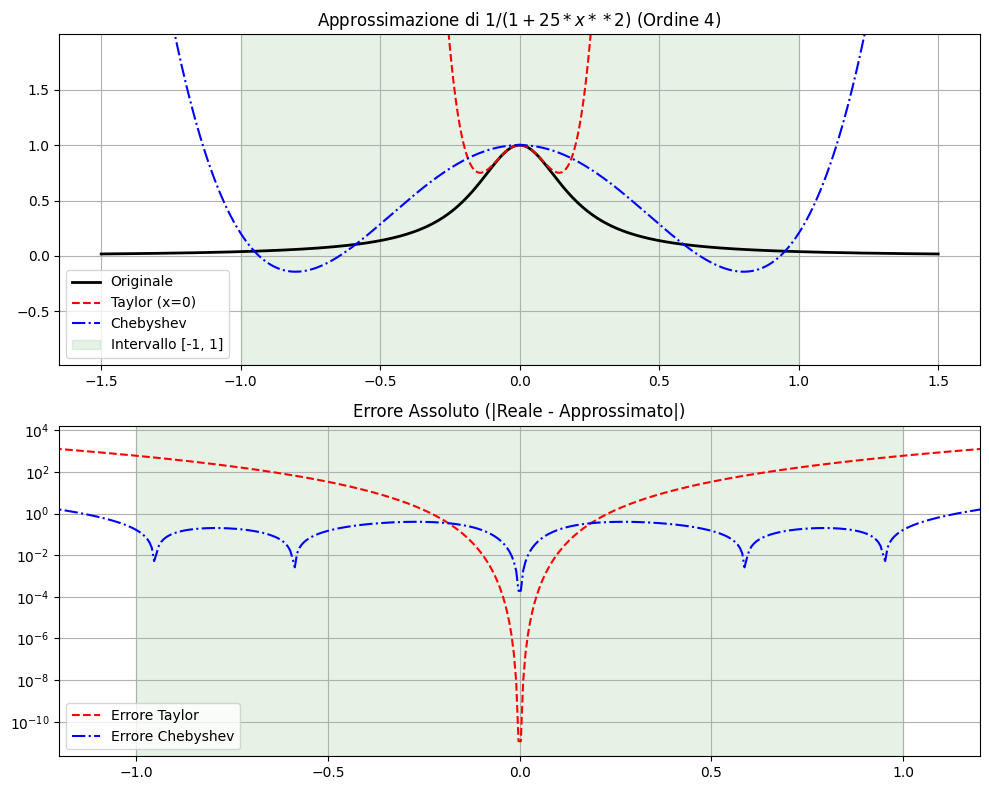
visualizza_grafico('1/(1+25*x**2)', 4)
| Caratteristica | Serie di Taylor | Serie di Chebyshev |
| Precisione in $x=0$ | perfetta | Piccola discrepanza |
| Precisione ai bordi ($x=\pm 1$) | L'errore cresce rapidamente | L'errore è distribuito uniformemente |
| Errore Massimo | Circa $0.218$ (in $x=1$) | Circa $0.006$ |
Il motivo per cui Chebyshev è così importante nell'IA e nel calcolo numerico è la sua proprietà di Minimax.Tra tutti i polinomi di grado $n$ che hanno il coefficiente del termine di grado massimo uguale a $1$, il polinomio $T_n(x) / 2^{n-1}$ è quello che ha il valore massimo più piccolo possibile nell'intervallo $[-1, 1]$.
Quindi volendo approssimare una funzione complicata con un polinomio in modo che l'errore massimo sia il più piccolo possibile, la soluzione sarà legata ai polinomi di Chebyshev. Essi distribuiscono l'errore in modo uniforme ("equioscillazione"), evitando che l'approssimazione sia perfetta al centro ma pessima ai bordi.
Ad esempio interpolando una funzione come $f(x) = \frac{1}{1+25x^2}$ usando punti equispaziati si ottengono delle oscillazioni selvagge ai bordi, il "fenomeno di Runge". La soluzione è, anziché punti equispaziati, usare le radici dei polinomi di Chebyshev, chiamate Nodi di Chebyshev.
Questi punti sono più densi vicino ai bordi dell'intervallo e più radi al centro, come quando si proiettano dei punti equidistanti lungo una semicirconferenza sul diametro: i punti che ottieni sul diametro sono i nodi di Chebyshev. Utilizzando questi nodi, l'errore di interpolazione viene minimizzato drasticamente e le oscillazioni di Runge spariscono.
In conclusione le seguenti sono importanti applicazioni di questi polinomi.
- Sviluppo in Serie di Chebyshev.
Proprio come la serie di Fourier usa basi di $\sin$ e $\cos$, si può sviluppare una funzione in serie di $T_n(x)$. Per le funzioni non periodiche, questa serie converge molto più velocemente della serie di Taylor. - Compressione di Funzioni.
Nelle calcolatrici e nelle librerie matematiche, come ad esempio quelle che calcolano sin(x) o exp(x) nei processori, spesso si usano approssimazioni di Chebyshev per ottenere la massima precisione con il minimo numero di operazioni. - Metodi Spettrali.
In fluidodinamica computazionale, ad esempio per simulare il meteo o il flusso d'aria su un'ala, i polinomi di Chebyshev sono usati per risolvere equazioni differenziali con una precisione che supera di gran lunga i metodi tradizionali a differenze finite.