Meccanica Quantistica

Quello delle basi ortonormali è il linguaggio naturale con cui la realtà quantistica si lascia descrivere.
Ogni base ortonormale corrisponde a un possibile “quadro di riferimento informazionale” sul sistema e il formalismo quantistico può essere visto come la teoria delle trasformazioni unitarie tra tali quadri.

La teoria delle basi ortonormali negli spazi di Hilbert fornisce alla meccanica quantistica una struttura lineare per la sovrapposizione degli stati, un prodotto interno per definire le probabilità, la completezza per garantire la stabilità analitica.
In tale formalismo gli stati fisici sono vettori, gli osservabili sono operatori, le misure sono proiezioni, le probabilità sono norme, l’evoluzione è una rotazione che preserva l’ortogonalità. Oltre all’evoluzione temporale, si possono descrivere le simmetrie e la connessione tra rappresentazioni (posizione, momento, spin).

La formulazione matematica della meccanica quantistica si basa su uno spazio vettoriale con prodotto interno che potrà avere da solo due dimensioni a infinite e dunque essere uno spazio di Hilbert complesso separabile. In ogni caso indicheremo con \( \mathcal{H} \) questo spazio.
Uno stato puro è rappresentato da un vettore di $\mathcal{H}$, la funzione d'onda, indicato con \( |\psi\rangle\), con il simbolo \( |\;\cdot\;\rangle\) detto ket nella notazione di Dirac, definito a meno di una fase complessa inosservabile: \[ |\psi\rangle \sim e^{i\theta} |\psi\rangle. \] Il prodotto interno, antilineare nel primo argomento e lineare nel secondo, \[ \langle \phi | \psi \rangle \in \mathbb{C} \] è la proiezione di $∣ψ⟩$ su $∣\phi⟩$, l’ampiezza di probabilità di trovare il sistema nello stato $∣\phi⟩$ quando si trova in $∣ψ⟩$.
L'operatore $$⟨\phi∣=∣\phi⟩^T$$ con il simbolo \(\langle\;\cdot\;|\) detto bra, è un elemento dello spazio duale $H^*$ dei funzionali lineari continui: \[⟨\phi∣\;: | \psi \rangle \longrightarrow \langle \phi | \psi \rangle.\]

I vettori che rappresentano gli stati fisici sono normalizzati: \[ \|\psi\| = \sqrt{|\langle \psi | \psi \rangle|} = 1, \] e ciò assicura che la probabilità totale si conserva. Il suo quadrato \(|\langle \psi | \psi \rangle|\) rappresenta la densità di probabilità che si verifichi quello stato.

Una famiglia \( \{ |e_n\rangle \}_{n\in I} \subset \mathcal{H} \) per cui

1. \( \langle e_m | e_n \rangle = \delta_{mn} \) (ortonormalità),
2. \( \overline{\mathrm{span}}\{ |e_n\rangle \} = \mathcal{H} \) (completezza),

è una base ortonormale. Quando $I$ è numerabile, lo spazio $\mathcal{H}$ si dice separabile.
Si osservi che \[\langle \phi | \psi \rangle =\sum_n\langle \phi | e_n \rangle \langle e_n | \psi \rangle,\] da cui \[ | \psi \rangle =\sum_n | e_n \rangle \langle e_n | \psi \rangle, \quad \displaystyle\langle \phi | =\sum_n\langle \phi | e_n \rangle \langle e_n |.\] Si può scrivere perfino \[ | =\sum_n | e_n \rangle \langle e_n |.\] Questa relazione di chiusura si può scrivere anche: \[ \sum_{n} |e_n\rangle \langle e_n| = \mathbb{I}, \] dove la somma converge nel senso forte all'identità come conseguenza della completezza.
L'operatore $P_n=|e_n\rangle \langle e_n|$ è il proiettore sullo spazio unidimensionale generato da $∣e_n​⟩$, tale che \[P_n\psi=|e_n\rangle \langle e_n|\psi\rangle\] cioè un vettore che ha direzione $∣e_n​⟩$ ed è suo multiplo secondo \( \langle e_n|\psi\rangle;\) inoltre, considerando anche che \[\sum_nP_n =\mathbb I,\] si ha che $⟨ψ∣P_n​ψ⟩=\langle\psi|e_n\rangle \langle e_n|\psi\rangle=|⟨e_n​∣ψ⟩|^2$ è la probabilità di passare allo stato $∣e_n​⟩$ quando il sistema si trova nello stato $∣ψ⟩$. per cui se il ket è unitario il proiettore è idempotente.
Ogni vettore ammette un’espansione unica rispetto a una base ortonormale \( \{ |e_n\rangle \} \): \[ |\psi\rangle = \sum_{n} \langle e_n | \psi \rangle |e_n\rangle, \] e di conseguenza per la sua norma: \[ \| |\psi\rangle\|^2 = \sum_n |\langle e_n | \psi \rangle|^2. \]

Un'osservabile, come la posizione, l'impulso, lo spin o l'energia, cioè gli aspetti del fenomeno fisico suscettibili di essere misurate, è rappresentata da un operatore lineare autoaggiunto limitato \(A : \mathcal{H} \to \mathcal{H},\) cioè \(\langle \phi | A\psi \rangle=\langle A\phi | \psi \rangle^*, \;\; \forall\phi,\psi\in\mathcal{H}, \) tale che i suoi autovalori sono numeri reali e i suoi autovettori formano una base ortonormale.
Nella notazione di Dirac \( A\psi\) si indica \( A|\psi\rangle\) e \(\langle \phi | A\psi \rangle\) si indica \(\langle \phi | A |\psi \rangle\).
Indicando con \( \{ |a_n\rangle \}\) la base degli autovettori, o autostati, dell'osservabile \(A\) e \( \{ a_n\}\) i rispettivi autovalori, allora \[A|a_n \rangle=a_n|a_n \rangle.\] Allo spazio dei funzionali lineari da \(\mathcal{H}\) a \(\mathbb C\), indicato con \(\mathcal{H}^*\), appartengono anche \(\langle \psi|\) e i proiettori $P_n=|e_n\rangle \langle e_n|$ sullo spazio unidimensionale generato da $∣e_n​⟩$, idempotenti, autoaggiunti e che hanno solo 0 e 1 per autovalori.

• I possibili risultati della misurazione di un osservabile sono i suoi autovalori.
• Se il sistema si trova nello stato \(|\psi\rangle\) che è un autovettore - o autostato - dell'osservabile, allora la misura dell'osservabile darà certamente come risultato l'autovalore associato a quell'autovettore.
• Se nello stato descritto da \(|\psi\rangle\) si effettua una misurazione relativa a un osservabile ottenendo una certa misura, autovalore dell'osservabile, immediatamente lo stato "collassa" nell'autostato associato a quell'autovalore ovvero diventa la proiezione dello stato nel sottospazio associato a quell'autovalore (riduzione del pacchetto d'onda).
  Indicato con \(A\) l'osservabile, lo stato \(∣𝜓⟩\) cambia secondo la regola di Born: \[|𝜓⟩ \longrightarrow \frac{𝑃_n∣𝜓⟩}{⟨𝜓∣𝑃_n∣𝜓⟩}=\frac{|a_n\rangle \langle a_n | \psi \rangle}{|\langle a_n | \psi \rangle|^2}\] dove \(𝑃_n\) è il proiettore sull’autospazio dell’autovalore misurato. Si tratta di una trasformazione non lineare, non unitaria, non invertibile, che quindi non può essere rappresentata come un operatore lineare.
• La probabilità che per effetto di una misurazione dell’osservabile \(A\) lo stato del sistema \(|\psi\rangle\) collassi in \(|a_n\rangle\), autovettore di \(A\), è \(|\langle a_n | \psi \rangle|^2=\langle \psi |P_n| \psi \rangle.\)
  Dunque il valor medio dei possibili risultati delle misurazioni è \(\displaystyle\sum_n |\langle a_n | \psi \rangle|^2a_n=\sum_n\langle \psi |P_n| \psi \rangle a_n.\)
• Indicando con \(P_n\) il proiettore associato all'autovalore \(a_n\) ne deriva la decomposizione spettrale dell'osservabile \( A\) \[A=\sum_na_nP_n= \sum_n a_n |a_n\rangle \langle a_n|.\] Quando \(A\) è una matrice hermitiana ciò è come dire che \(\displaystyle A=UDU^{\dagger }\) dove \(U\) è la matrice che ha per colonne gli autovettori e \(D\) la matrice diagonale degli autovalori.
  Anche l'espressione \(\langle\psi |A|\psi\rangle\) esprime il valor medio dei possibili risultati delle misurazioni di \(A.\)
• Se \(A\) è un osservabile, l'espressione \(Tr(A)=\sum_n\langle a_n | A |a_n \rangle,\) detta traccia dell'operatore \(A,\) è la somma degli autovalori, invariante sotto un cambio di base.

Per misurare l’energia di un sistema, ad esempio, si considera l’hamiltoniana come osservabile. A seguito di un processo di misurazione si ottiene con una certa probabilità una misura che coincide con uno degli autovalori e inoltre, immediatamente, il collasso dello stato sull'autostato associato a questa misura. Una misurazione è quindi un processo irreversibile che trasforma uno stato in un autostato dell'osservabile, lo trasforma irreversibilmente perché estrae informazione.

Due osservabili \(A\) e \(B\) si dicono compatibili se ammettono un sistema completo di autovettori comuni. E’ possibile dimostrare che questa richiesta è equivalente alla condizione \(AB = BA.\)
Gli stati posizione \( |x\rangle \) soddisfano la forma generalizzata di ortonormalità: \[ \langle x | x' \rangle = \delta(x - x'), \] \[ \int_{\mathbb{R}} |x\rangle \langle x| \, dx = \mathbb{I}. \] I valori della funzione d’onda sono: \[ \psi(x) = \langle x | \psi \rangle. \] Gli stati momento \( |p\rangle \) soddisfano: \[ \langle p | p' \rangle = \delta(p - p'), \] \[ \int_{\mathbb{R}} |p\rangle \langle p| \, dp = \mathbb{I}. \] La trasformazione posizione $\longleftrightarrow$ momento è unitaria: \[ \psi(p) = \frac{1}{\sqrt{2\pi\hbar}} \int e^{-ipx/\hbar} \psi(x) \, dx. \] Gli autostati della posizione non coincidono con quelli dell’impulso. Le due basi sono legate da una trasformazione, la trasformata di Fourier, ma non possono essere diagonalizzate simultaneamente.
Questo fatto geometrico è all’origine del

L’indeterminazione non nasce dunque da un limite tecnico ma da una struttura matematica dello spazio degli stati.

Se \( \{|e_n\rangle\} \) e \( \{|f_n\rangle\} \) sono due basi ortonormali, allora: \[ |f_n\rangle = U |e_n\rangle. \] Le componenti di un vettore \(\psi\) cambiano come: \[ \langle f_n | \psi \rangle = \sum_m \langle f_n | e_m \rangle \, \langle e_m | \psi \rangle. \] La matrice \(U = (U_{n,m}) = (\langle f_n | e_m \rangle)\) è unitaria: \[ \sum_m U_{n,m} U_{n',m}^* = \delta_{nn'} \] ovvero \[ U^\dagger U = U U^\dagger = \mathbb{I}. \]

Fisicamente, l'evoluzione temporale può essere interpretata come una rotazione rigida nello spazio di Hilbert, che preserva le probabilità ridistribuendo le ampiezze tra gli stati di base.
Le basi associate a direzioni diverse sono collegate da matrici unitarie di SU(2).

Una base ortonormale canonica per un sistema a due stati come gli spin \(1/2\) di un elettrone o la polarizzazione di un fotone è: \[ |\uparrow_z\rangle = \begin{pmatrix}1 \\ 0\end{pmatrix}, \qquad |\downarrow_z\rangle = \begin{pmatrix}0 \\ 1\end{pmatrix}. \] Lo stato generico \(α|\uparrow_z\rangle+ β\downarrow_z\rangle\) dovrà avere \(α^2+ β^2=1 \). Esistono poi solo 4 operatori hermitiani, quindi autoaggiunti, linearmente indipendenti, una base dello spazio delle matrici 2×2 hermitiane: l'identità e le tre matrici di Pauli.
Nel seguente esempio Python con SymPy a partire dalle matrici di Pauli, si costruiscono le basi di autostati e si verificano ortonormalità e unitarietà del cambio di base.

Mostriamo di seguito come un vettore stato viene espresso in due basi diverse $z$ e $x$ per spin $1/2$. ovvero Possiamo infine considerare l'osservabile 'spin lungo x' e la misura che, a partire da uno stato iniziale che non è un autostato, produce risultati probabilistici.

Volendo considerare l'energia in un campo magnetico con direzione z si deve considerare l'Hamiltoniano \(H=−γB⋅S,\) dove \(S=\frac{ℏ}{2}σ,\)

Volendo esaminare la dinamica di un elettrone che ruota attorno alla direzione di un campo magnetico B, la soluzione è \(|ψ(t)⟩=e^{-iHt/ℏ}|ψ(0)\rangle.\)

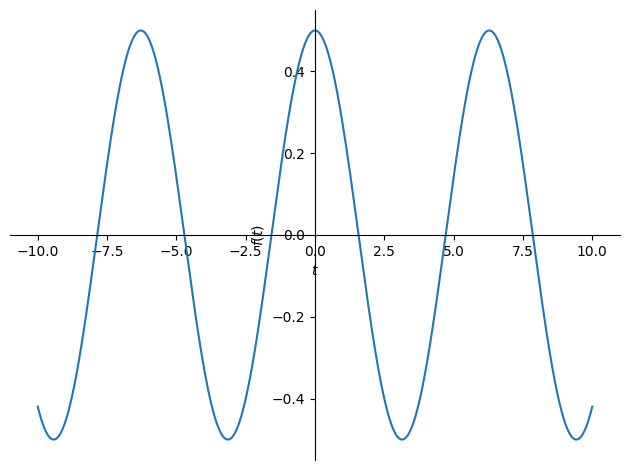
Si ha il fenomeno Precessione di Larmor.

Un altro esempio è quello di un elettrone soggetto a un campo elettrico uniforme \( \mathbf{E} \) lungo \(x\), il cui potenziale è \(V(x) = -e E x\). La dinamica è governata dall’Hamiltoniana: \[ \hat H = -\frac{\hbar^2}{2m}\frac{d^2}{dx^2} - e E x \] che definisce completamente il problema quantistico.
Lo stato dell’elettrone è un vettore: \[ |\psi\rangle \in \mathcal{H} = L^2(\mathbb{R}) \] Dall'equazione di Schrödinger \[ i\hbar \frac{\partial \psi}{\partial t}=\hat H \psi \] formalmente si ricava \[ |\psi(t)\rangle = e^{-i\hat H t/\hbar} |\psi(0)\rangle. \] Espandendo su una base ortonormale discreta \({|e_n\rangle}\) di autostati di \(\hat H\): \[ |\psi(t)\rangle = \sum_n \langle e_n | \psi(0) \rangle e^{-i e_nt/\hbar} |e_n\rangle \] Anziché la traiettoria, un concetto della meccanica classica che non esiste nella meccanica quantistica, si sceglie una base ortonormale, ognuna corrispondente a una diversa “lente” osservativa, in cui rappresentare lo stato. Ad esempio:

• la base \(|x\rangle\) delle posizioni in cui \(\psi(x,t) = \langle x | \psi(t) \rangle,\) per cui il “moto” dell’elettrone è ora lo scorrere delle ampiezze \(\psi(x,t)\), una redistribuzione di probabilità;
• una base ortonormale generalizzata di autostati \(|E\rangle\) dell’Hamiltoniana, per cui \(\hat H |E\rangle = E |E\rangle,\) che si riduce con un cambiamento di variabile a un'equazione di Airy le cui soluzioni sono funzioni di Airy, che diagonalizzano l’evoluzione temporale, in cui dall'espansione \[ |\psi(t)\rangle = \int \langle E|\psi(0)\rangle e^{-iEt/\hbar} |E\rangle dE \] possiamo ricostruire la funzione d’onda nello spazio delle posizioni come \[\psi(x,t) = \langle x|\psi(t)\rangle = \int \langle x|E\rangle\langle E|\psi(0)\rangle e^{-iEt/\hbar} dE\] dove il campo elettrico è “assorbito” nella struttura della base, è dentro il cambiamento di variabile che porta all'equazione di Airy, e il moto è solo una rotazione di fase;
• la base \(|p\rangle\) degli impulsi, continua, collegata alla base della posizione tramite una trasformata di Fourier, per cui \(\phi(p,t) = \langle p | \psi(t) \rangle\) e il potenziale lineare produce: \[ i\hbar \frac{\partial \phi}{\partial t}=\left(\frac{p^2}{2m}+ i e E \hbar \frac{\partial}{\partial p} \right)\phi \] da cui emerge il fatto notevole che il campo elettrico genera una traslazione nello spazio degli impulsi e il valore medio dell’impulso vale \[ \frac{d}{dt}\langle p \rangle = -eE \] cioè la seconda legge di Newton in media, mentre lo stato resta un vettore in uno spazio ortonormale.

La meccanica quantistica non descrive il moto nello spazio fisico ma nello spazio delle funzioni. Se nel campo elettrico classico l’elettrone segue una parabola, nel formalismo quantistico la parabola è sostituita da una traslazione della distribuzione di probabilità descritta nel linguaggio fornito dalle basi ortonormali. Il moto emerge dai valori medi, dai limiti semiclassici e dalle proiezioni su basi appropriate.

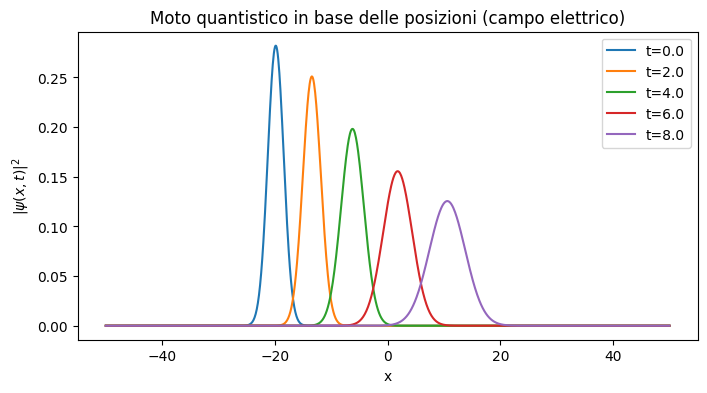
In Python possiamo simulare l’evoluzione della funzione d’onda \(ψ(x,t)=⟨x∣ψ(t)⟩\) del “moto” di un elettrone in un campo elettrico uniforme nella base delle posizioni. L’obiettivo non è la precisione fisica estrema, ma rendere visibile il ruolo della base delle posizioni: il moto come traslazione e deformazione della densità di probabilità.