Wavelets
In analisi dei segnali e nei dati reali risulta utile una base ortonormale che sia anche
- localizzata nel tempo o spazio, cioè non nulla in un insieme limitato (compatta), permetta di rappresentare caratteristiche locali modificando pochi coefficienti e per cui le matrici degli operatori differenziali siano sparse,
- multirisoluzione, con diverse scale di dettaglio capace di rappresentare discontinuità e strutture locali.
Le Wavelet nascono come costruzione di basi ortonormali adattate alla località e multirisoluzione.
Punto di partenza è una wavelet "madre" \({\displaystyle \psi \in L^{2}(\mathbb {R} )}\) con
- \({\displaystyle \int _{-\infty }^{+\infty }|\psi (t)|\ ^{2}\,dt=1},\)
- \({\displaystyle \int _{-\infty }^{+\infty }|\psi \ (t)|\,dt<+\infty }\), cioè \({\displaystyle \psi \in L^{1}(\mathbb {R} )}\) è finita,
- \({\displaystyle \int _{-\infty }^{+\infty }\psi \ (t)\,dt=0}\), cioè a media nulla.
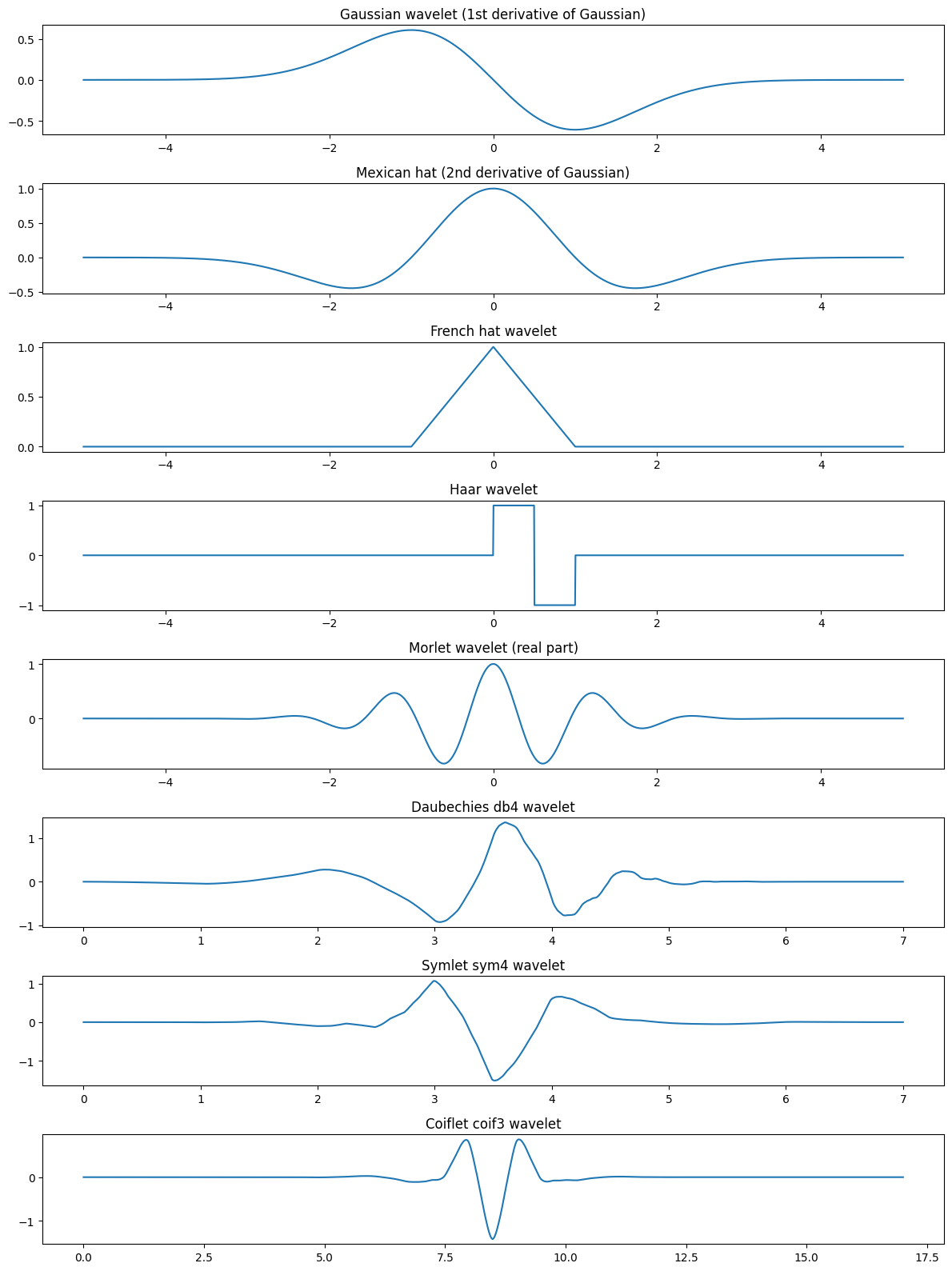
import pywt
# Dominio comune
t = np.linspace(-5, 5, 2000)
# 1. Gaussian wavelet (prima derivata della gaussiana)
gaussian_wave = -t * np.exp(-t**2 / 2)
# 2. Mexican hat (seconda derivata della gaussiana)
mexican_hat = (1 - t**2) * np.exp(-t**2 / 2)
# 3. French hat (triangolare)
french_hat = np.maximum(1 - np.abs(t), 0)
# 4. Haar wavelet
haar = np.zeros_like(t)
haar[(t >= 0) & (t < 0.5)] = 1
haar[(t >= 0.5) & (t < 1)] = -1
# 5. Morlet wavelet (parte reale)
omega0 = 5
morlet = np.cos(omega0 * t) * np.exp(-t**2 / 2)
# 6. Daubechies (db4)
db4 = pywt.Wavelet('db4')
phi_db4, psi_db4, x_db4 = db4.wavefun(level=8)
# 7. Symlet (sym4)
sym4 = pywt.Wavelet('sym4')
phi_sym4, psi_sym4, x_sym4 = sym4.wavefun(level=8)
# 8. Coiflet (coif3)
coif3 = pywt.Wavelet('coif3')
phi_coif3, psi_coif3, x_coif3 = coif3.wavefun(level=8)
plt.figure(figsize=(12, 16))
plt.subplot(8,1,1)
plt.plot(t, gaussian_wave)
plt.title("Gaussian wavelet (1st derivative of Gaussian)")
plt.subplot(8,1,2)
plt.plot(t, mexican_hat)
plt.title("Mexican hat (2nd derivative of Gaussian)")
plt.subplot(8,1,3)
plt.plot(t, french_hat)
plt.title("French hat wavelet")
plt.subplot(8,1,4)
plt.plot(t, haar)
plt.title("Haar wavelet")
plt.subplot(8,1,5)
plt.plot(t, morlet)
plt.title("Morlet wavelet (real part)")
plt.subplot(8,1,6)
plt.plot(x_db4, psi_db4)
plt.title("Daubechies db4 wavelet")
plt.subplot(8,1,7)
plt.plot(x_sym4, psi_sym4)
plt.title("Symlet sym4 wavelet")
plt.subplot(8,1,8)
plt.plot(x_coif3, psi_coif3)
plt.title("Coiflet coif3 wavelet")
plt.tight_layout()
plt.show()
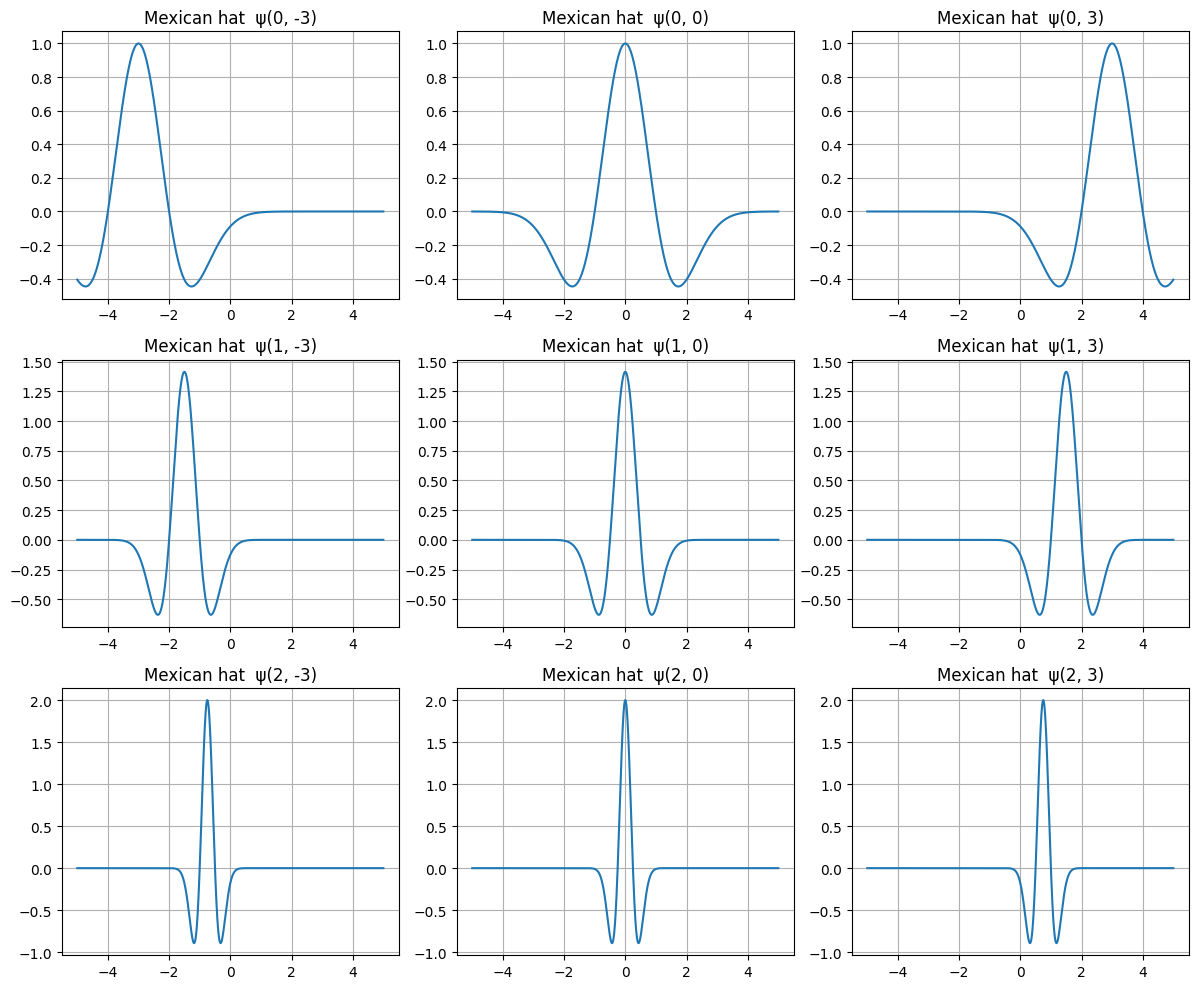
A partire dalla wavelet madre si costruisce la famiglia \[ψ_{j,k}(t)=2^{j/2}ψ(2^jt-k)\] dove:
- j è l'elemento di scala (risoluzione),
- k è l'elemento di scala traslazione,
- il fattore $2^{j/2}$ preserva la norma: $\|ψ_{j,k}\|=1.$
# Mexican hat (seconda derivata della gaussiana)
def mexican_hat(t):
return (1 - t**2) * np.exp(-t**2 / 2)
# Wavelet scalata e traslata: ψ_{j,k}(t)
def ψ(t, j, k):
return 2**(j/2) * mexican_hat(2**j * t - k)
# Dominio
t = np.linspace(-5, 5, 2000)
# Scelte di scale e traslazioni
scales = [0, 1, 2] # j
translations = [-3, 0, 3] # k
plt.figure(figsize=(12, 10))
plot_index = 1
for j in scales:
for k in translations:
plt.subplot(len(scales), len(translations), plot_index)
plt.plot(t, ψ(t, j, k))
plt.title(f"Mexican hat ψ(j={j}, k={k})")
plt.grid(True)
plot_index += 1
plt.tight_layout()
plt.show()
Non ogni famiglia wavelet è una base ortonormale di $L_2$; lo sono ma molte di quelle usate in pratica (Haar, Daubechies, Symlet, Coiflet)
La Multiresolution Analysis (MRA), cuore delle wavelet ortonormali, permette di “vedere” un segnale a diverse scale proprio come con un microscopio ingrandisce progressivamente. Una MRA è una catena di sottospazi \(\{V_j\}_{j\in\mathbb Z}\) tale che:
- $\dots\subset V_{-1}\subset V_0 \subset V_1 \subset \dots$, ovvero ogni livello contiene più dettagli del precedente;
- \(\displaystyle ⋃_jV_j\) è denso in \(L^2(\mathbb R)\), ovvero a risoluzione infinita si può rappresentare qualunque funzione,
- $⋂Vj=\{0\}$, ovvero a risoluzione infinitamente grossolana non rimane nulla;
- \(f(t)\in V_j\iff f(2t)\in V_{j+1}\), invarianza per dilatazione ovvero passare da \( V_j\) a \(V_{j+1}\) significa “raddoppiare la risoluzione”;
- esiste una funzione \(𝜙\) (scaling function) che non abbia media nulla tale che \(\{2^{j/2}𝜙(2^j𝑥−𝑘)\}_{𝑘∈𝑍}\) è una base ortonormale di \(𝑉_j\) mentre \(\{2^{j/2}\psi(2^j𝑥−𝑘)\}_{𝑘∈𝑍}\) è base ortonormale di \(W_j\), ovvero \(𝑉_𝑗\) sono le approssimazioni generate da \(𝜙_{j,𝑘}\) e \(𝑊_𝑗\) sono i dettagli generati da \(\psi_{j,𝑘}\).
Relazione chiave è la decomposizione ortogonale: \[V_{j+1}=V_j⊕W_j\] dove \(W_j=\{u\in V \text{ tali che }\langle u,ϕ_{j,k} \rangle=0,\; \forall k\}\) è lo spazio dei dettagli, quelli che mancano per passare da risoluzione \(𝑗\) a risoluzione \(𝑗+1\), che ha come base ortonormale le wavelet \(\{ψ_{j,k}\}\) e \(⊕\) è somma ortogonale. L’intero spazio è: \[L^2(\mathbb R)=V_0 ⊕⨁_{j=0}^∞W_j\] Perciò ogni segnale $f(t)$ può essere scritto come: \[\displaystyle f(t)=\sum_kc_kϕ_{0,k}(t)+\sum_{j,k}d_{j,k}ψ_{j,k}(t)\] con coefficienti: \[d_{j,k}=⟨f,ψ_{j,k}⟩\] e grazie all’ortonormalità \[\displaystyle \|f\|^2=\sum_k∣c_k∣^2+\sum_{j,k}∣d_{j,k}∣^2\] con il rumore distribuito sulle scale fini.
La MRA, che quindi unisce analisi funzionale, geometria e teoria dei segnali, permette di analizzare segnali non stazionari separando trend, oscillazioni e rumore, fare denoising, forecasting multiscala, nonché compressioni come JPEG2000.
La Discrete Wavelet Transform (DWT) è una trasformazione lineare che scompone un segnale discreto in approssimazioni (componenti a bassa frequenza) e dettagli (componenti ad alta frequenza)
utilizzando una wavelet madre \(\psi\) e una scaling function \(\phi\), derivate da una MRA.
La DWT, che è
- ortogonale (per wavelet ortonormali),
- non ridondante,
- perfettamente ricostruibile,
- multiscala,
- computazionalmente efficiente \(O(N)\),
La DWT a un livello fa:
- convoluzione con \(h\) per produrre approssimazioni \[ A_1(n) = \sum_k f(k)\, h(2n - k) \]
- convoluzione con \(g\) per produrre dettagli \[ D_1(n) = \sum_k f(k)\, g(2n - k) \]
- decimazione (downsampling) per cui si tiene un campione su due, dimezzata la lunghezza,
- si ripete il processo su \(A_1\).
Dopo \(J\) livelli ottieni si ottiene la decomposizione multiscala \[ f = A_J + D_J + D_{J-1} + \dots + D_1 \] dove \(A_J\) è la componente più lenta (trend) e i \(D_j\) sono i dettagli a scala \(2^{-j}.\) Azzerando i dettagli e ricostruendo ottieni una approssimazione liscia. La ricostruzione usa i filtri di sintesi \(h'\), filtro passa-basso di ricostruzione, e \(g'\), filtro passa-alto di ricostruzione. La ricostruzione a un livello fa:
- upsampling, (inserimento di zeri),
- convoluzione con h' e g',
- somma.
I filtri \(h,g\) derivano dalla scaling function \(\phi\) e dalla wavelet madre \(\psi\): \[ \phi(t) = \sqrt{2}\sum_{k} h(k)\,\phi(2t - k), \] \[ \psi(t) = \sqrt{2}\sum_{k} g(k)\,\phi(2t - k). \] Per wavelet ortonormali come Daubechies, Symlet, Coiflet vale la quadrature mirror relation (QMF): \[ g(k) = (-1)^{k}\, h(1-k) \] cioè il filtro g è ottenuto ruotando e alternando i segni del filtro h, condizione necessaria per avere: \[ V_{j+1} = V_j \oplus W_j \] Seguono due esempi.
- Per la wavelet Haar con scaling function: \[ \phi(t) = \begin{cases} 1 & 0 \le t < 1 \\ 0 & \text{altrove} \end{cases} \] La two‑scale relation è: \[ \phi(t) = \phi(2t) + \phi(2t - 1) \] Quindi: \[ h = \left[\frac{1}{\sqrt{2}},\; \frac{1}{\sqrt{2}}\right] \] Il filtro g si ottiene con la QMF: \[ g = \left[\frac{1}{\sqrt{2}},\; -\frac{1}{\sqrt{2}}\right] \]
- Per la wavelet Daubechies db2 (4 coefficienti) i coefficienti h sono determinati imponendo ortogonalità, 2 momenti nulli della wavelet, supporto minimo, ottenendo come risultato (non banale da derivare a mano) è: \[ h = \left[ \frac{1+\sqrt{3}}{4\sqrt{2}},\; \frac{3+\sqrt{3}}{4\sqrt{2}},\; \frac{3-\sqrt{3}}{4\sqrt{2}},\; \frac{1-\sqrt{3}}{4\sqrt{2}} \right] \] E g si ottiene con la QMF: \[ g[k] = (-1)^k h[3-k] \]
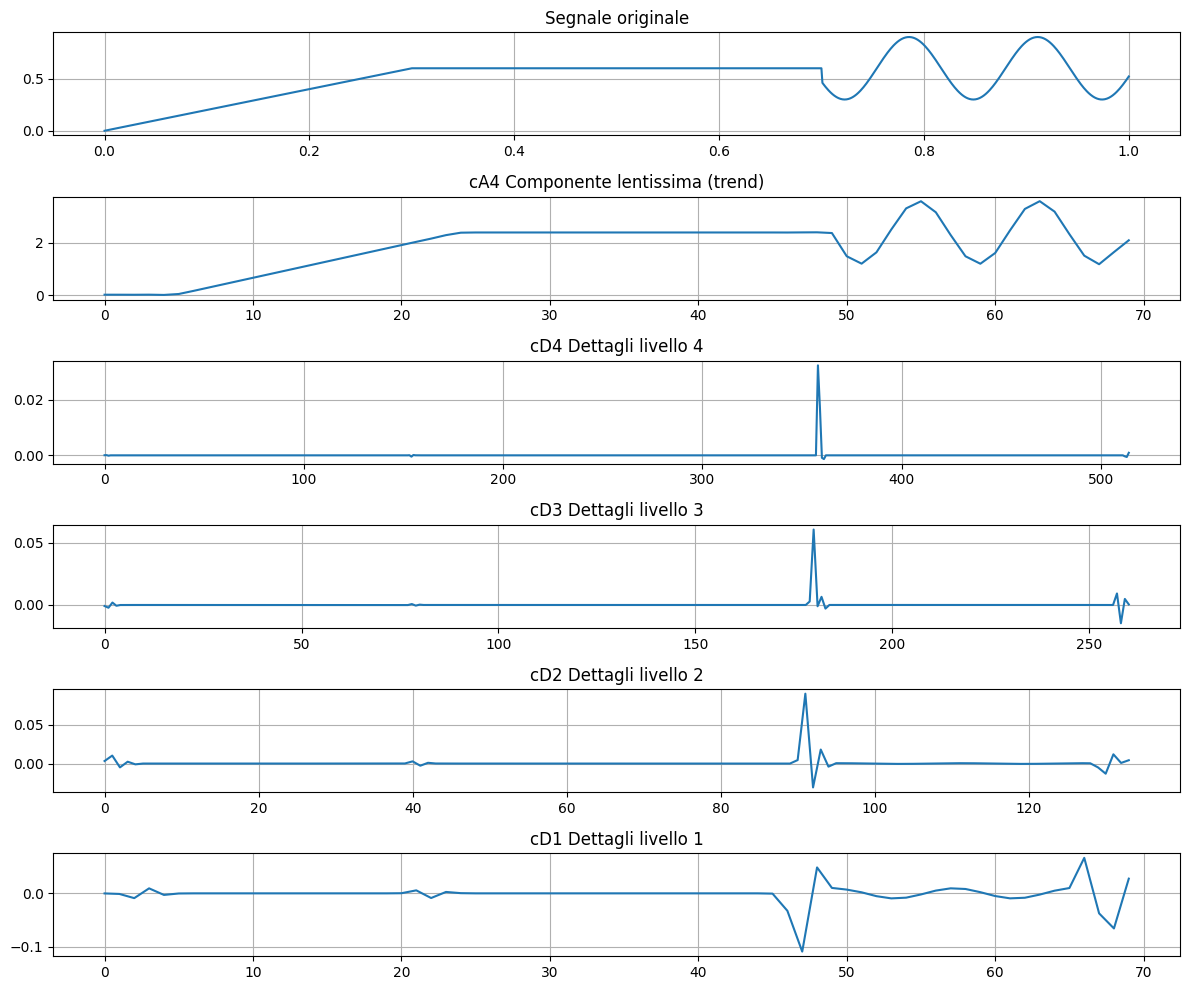
Un esempio semplice ma significativo dell’uso delle wavelet, in questo caso la Daubechies 4, è rilevare e localizzare discontinuità in un segnale, cosa che la trasformata di Fourier non fa bene perché lavora solo nel dominio delle frequenze.
Costruito un segnale liscio in alcuni tratti con una discontinuità netta e con un tratto oscillatorio
applichiamo poi la DWT per decomporre il segnale in approssimazioni e dettagli, evidenziare dove si trovano le discontinuità e confrontare il segnale originale con i coefficienti wavelet.
import pywt
# Costruzione del segnale
x = np.linspace(0, 1, 1024)
signal = np.piecewise(
x,
[x < 0.3, (x >= 0.3) & (x < 0.7), x >= 0.7],
[lambda x: 2*x, lambda x: 0.6, lambda x: 0.6 + 0.3*np.sin(50*x)]
)
# Coefficienti della Trasformata Wavelet Discreta (DWT) Daubechies 4
level = 4
coeffs = pywt.wavedec(signal, wavelet='db4', level=level)
plt.figure(figsize=(12, 10))
plt.subplot(6,1,1)
plt.plot(x, signal)
plt.title("Segnale originale")
plt.grid(True)
plt.subplot(6,1,2)
plt.plot(coeffs[0])
plt.title(f"cA{level} Componente lentissima (trend)")
plt.grid(True)
for i in range(level,0,-1):
plt.subplot(6,1,level-i+3)
plt.plot(coeffs[i])
plt.title(f"cD{i} Dettagli livello {i}")
plt.grid(True)
plt.tight_layout()
plt.show()
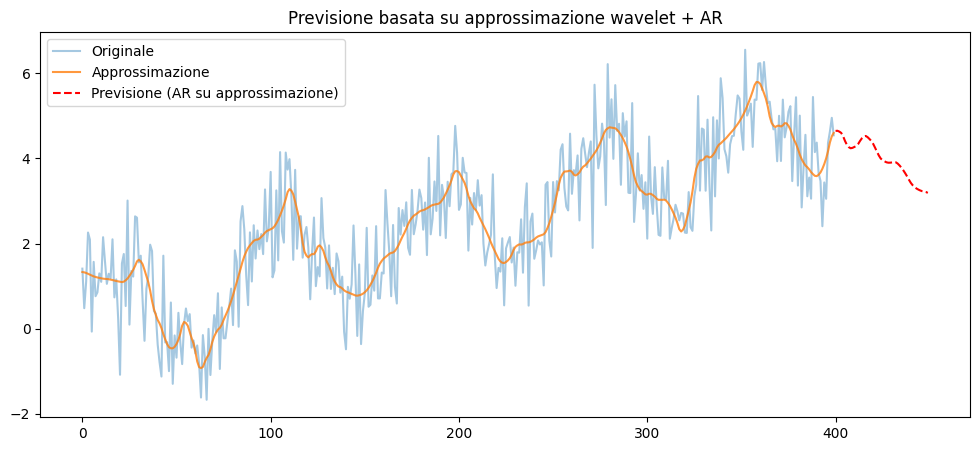
La MRA può essere usata come “microscopio” per una serie temporale reale per separarne automaticamente le componenti: un trend (scala molto larga), oscillazioni lente (cicli, stagionalità), oscillazioni veloci (rumore strutturato), rumore puro (scala finissima).
Una wavelet non guarda il segnale una sola volta ma più volte, ogni volta con una “lente” diversa:
- una lente larga che vede solo il comportamento globale (trend),
- una lente media che vede oscillazioni lente,
- una lente stretta che vede oscillazioni veloci,
- una lente strettissima che vede il rumore.
Dopo \(𝐽\) livelli:\[𝑥(𝑡)=𝐴_𝐽(𝑡)+𝐷_𝐽(𝑡)+𝐷_{𝐽−1}(t)+⋯+𝐷_1(𝑡)\]
dove \(𝐴_𝐽\) è la componente lentissima (trend), \(𝐷_𝐽\) le oscillazioni lente, \(𝐷_{𝐽−1}\) oscillazioni più veloci e così via fino a \(𝐷_{1}\) oscillazioni molto veloci (rumore).
La wavelet costruisce una base ortonormale dello spazio delle funzioni:
\[
\{ \phi_{J,k} \} \cup \{ \psi_{j,k} : j=1,\dots,J \}
\]
dove \(\phi\) sono funzioni “lente” (scaling functions) e \(\psi\) funzioni “veloci” (wavelet)
Le proiezioni del segnale su \(\phi\) danno il trend, quelle su \(\psi\) a scala grande le oscillazioni lente e quelle su \(\psi\) a scala piccola il rumore.
from statsmodels.tsa.ar_model import AutoReg
# 1. Serie temporale sintetica
np.random.seed(0)
n = 400
t = np.linspace(0, 10, n)
x = 0.5 * t + np.sin(3*t) + 0.3*np.sin(10*t) + 0.8*np.random.randn(n)
# 2. Decomposizione wavelet + denoising
wavelet, level = 'db4', 4
coeffs = pywt.wavedec(x, wavelet=wavelet, level=level)
coeffs_approx, level_approx = coeffs.copy(), 2
for i in range(level_approx, len(coeffs_approx)):
coeffs_approx[i] = np.zeros_like(coeffs_approx[i])
x_approx = pywt.waverec(coeffs_approx, wavelet)
# 3. Modello AR sulla serie denoised
lags = 10
model = AutoReg(x_approx, lags=lags).fit()
h = 50 # passi futuri
x_pred = model.predict(start=len(x_approx), end=len(x_approx)+h-1)
plt.figure(figsize=(12,5))
plt.plot(x, label="Originale", alpha=0.4)
plt.plot(x_approx, label="Approssimazione", alpha=0.8)
plt.plot(np.arange(n, n+h), x_pred, 'r--', label="Previsione (AR su approssimazione)")
plt.title("Previsione basata su approssimazione wavelet + AR")
plt.legend()
plt.show()
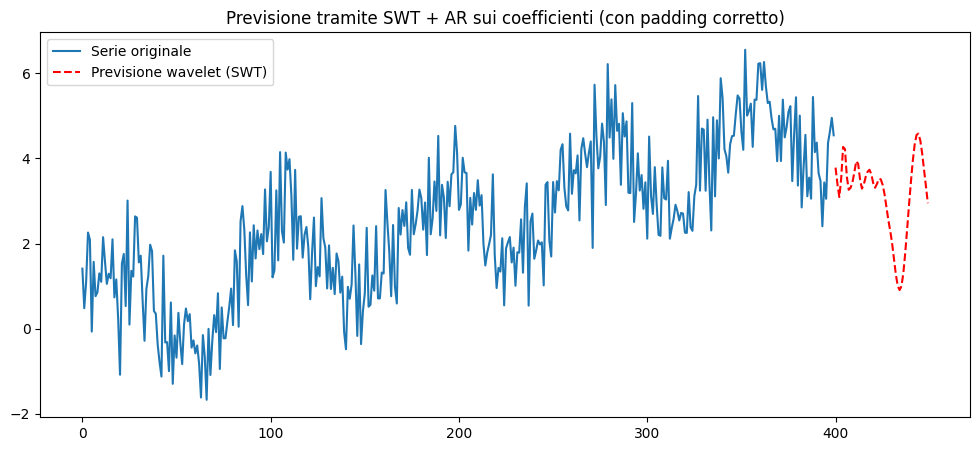
La Stationary Wavelet Transform (SWT) nasce per risolvere problemi della MRA relativi al denoising, al rilevamento di picchi, al forecasting multiscala e all'analisi di segnali non stazionari. Fa la stessa decomposizione della DWT, ma senza decimare e, per compensare la mancanza di decimazione, i filtri vengono dilatati a ogni livello.
Al livello \(j\) si applicano filtri \(h_j\) e \(g_j\) ottenuti “inserendo zeri” nei filtri originali e
si convolvono con il segnale senza decimare. Così \(A_j\) e \(D_j\) hanno la stessa lunghezza del segnale originale per tutti i livelli.
La SWT è coerente con la MRA, condivide la stessa struttura concettuale, ma non è una MRA nel senso classico.
Infatti nella SWT gli spazi non si “stringono”, non c’è decimazione, la rappresentazione è ridondante (molto più grande del segnale), è una MRA ridondante, non ortonormale, ma perfettamente coerente con la struttura multiscala.
# 2. SWT (Stationary Wavelet Transform)
wavelet, level = 'db4', 3
coeffs = pywt.swt(x, wavelet=wavelet, level=level)
# coeffs = [(cA_1, cD_1), (cA_2, cD_2), ..., (cA_level, cD_level)]
L = len(coeffs[0][0]) # lunghezza originale
step = 2**level # vincolo di lunghezza per iswt
# 3. Previsione dei coefficienti
h = 50 # passi futuri
coeffs_future = []
for (cA, cD) in coeffs:
# modello AR(5) per ciascun livello
model_A = AutoReg(cA, lags=5).fit()
model_D = AutoReg(cD, lags=5).fit()
# previsione
cA_future = model_A.predict(start=len(cA), end=len(cA)+h-1)
cD_future = model_D.predict(start=len(cD), end=len(cD)+h-1)
# estendiamo i coefficienti con le previsioni
cA_ext = np.concatenate([cA, cA_future])
cD_ext = np.concatenate([cD, cD_future])
coeffs_future.append((cA_ext, cD_ext))
# 4. Padding per rispettare il vincolo di iswt
# (lunghezza multipla di 2**level)
new_len = L + h
pad_len = (step - new_len % step) % step # quanto manca al prossimo multiplo
coeffs_padded = []
for (cA_ext, cD_ext) in coeffs_future:
cA_pad = np.concatenate([cA_ext, np.zeros(pad_len)])
cD_pad = np.concatenate([cD_ext, np.zeros(pad_len)])
coeffs_padded.append((cA_pad, cD_pad))
# 5. Ricostruzione con ISWT
x_future_full = pywt.iswt(coeffs_padded, wavelet)
# lunghezza totale ricostruita
L_rec = len(x_future_full)
# la parte finale corrisponde agli ultimi (h + pad_len) punti
# ma a noi interessano solo gli ultimi h (senza padding)
x_pred = x_future_full[L + pad_len : L + pad_len + h]
plt.figure(figsize=(12,5))
plt.plot(x, label="Serie originale")
plt.plot(np.arange(n, n+h), x_pred, 'r--', label="Previsione wavelet (SWT)")
plt.legend()
plt.title("Previsione tramite SWT + AR sui coefficienti (con padding corretto)")
plt.show()
Bibliografia
- Wavelet, From Wikipedia, the free encyclopedia
- Wavelet, da Wikipedia, l'encyclopedia libera
- Introduction to Wavelet Transform using Python, by Jake @Scicoding
- PyWavelets Documentation
- Using wavelets for time series forecasting: Does it pay off? by Schlüter, Stephan; Deuschle, Carola
- Note sulle ondicelle, di Paolo Caressa
- WAVELETS FOR KIDS A Tutorial Introduction, by Brani Vidakovic and Peter Mueller
- PyWavelets Documentation