Analisi delle Componenti Principali

Nell'intelligenza artificiale, e in particolare nel Machine Learning, la riduzione della dimensionalità è una necessità pratica: i dati, che rappresentano ad esempio immagini, sequenze genomiche, serie finanziarie, hanno migliaia o milioni di variabili, ma spesso molta di questa informazione è ridondante o è semplice rumore.
In un dataset ad alta dimensione, i dati sono inizialmente espressi nella base canonica, per cui ogni asse è una variabile misurata. Tuttavia, questa base raramente è la più efficiente per descrivere la struttura del fenomeno.
Obiettivo della Principal Component Analysis (PCA) è trovare una nuova base ortonormale $\{\mathbf{u}_1, \mathbf{u}_2, \dots, \mathbf{u}_n\}$ tale che:

1. il primo vettore \(\mathbf{u}_1\), detto prima componente principale, punti nella direzione di massima varianza, dove i dati sono più "spalmati", dove c'è più ricchezza di informazione,
2. il secondo vettore \(\mathbf{u}_2\), detto seconda componente principale, sia ortogonale al primo e catturi la massima varianza rimanente,
3. ... e così via.

Geometricamente la PCA è una rotazione dello spazio che allinea i dati con una base ortonormale ottimale in modo che la proiezione sulle prime componenti principali conserva la forma, elimina le distorsioni, riduce la dimensionalità, mantiene la struttura essenziale.
Ad esempio data una nuvola di punti che forma un cilindro inclinato nello spazio in 3 dimensioni, le sue proiezioni sui piani della base canonica non forniscono una scomposizione adatta per una chiara ricostruzione della forma complessiva. La PCA trova come prima componente di un nuovo rierimento la direzione lungo cui la forma è più allungata, l’asse del cilindro, come seconda componente la direzione di massima variazione residua e come terza quella ortogonale alle prime due. Così proiettando la forma sulle prime due componenti principali si ottiene una vista perfettamente allineata con la struttura, una rappresentazione 2D che conserva quasi tutta la geometria.
La PCA ruota cioè la forma nello spazio per guardarla “dal punto di vista giusto”.
In statistica, la varianza totale dei dati è l'analogo dell'energia di un segnale in fisica e l'analogo dell'informazione. L'identità di Parseval ci garantisce che se cambiamo base verso una base ortonormale come quella delle componenti principali, la varianza totale rimane invariata, ovvero sappiamo esattamente quanta informazione stiamo trattando.
Se poi ad esempio le prime 3 componenti principali catturano il 95% della varianza totale, l'energia del dataset, possiamo decidere di proiettare tutti i nostri dati solo su questo sottospazio di dimensione 3 scartando le altre n-3 dimensioni.
Passiamo così da un problema computazionalmente complesso a uno meglio gestibile, eliminando il rumore solitamente assocoato alle componenti con varianza minima.

Supponiamo dunque di avere un dataset con $p$ variabili $\mathbf{x}_1, \mathbf{x}_2, \dots, \mathbf{x}_p$ (features) ciascuna composta da $n$ osservazioni $x_{1,i},x_{2,i},\dots,x_{n,i}.$ che conviene considerare centrate intorno alla media, considerare cioè $χ_{1,i}-\overline{χ_i},x_{2,i}-\overline{χ_i},\dots,χ_{n,i}-\overline{χ_i}$ piuttosto che le osservazioni originarie $\mathbf{χ}_i$, poichè così

• la varianza è $var(\mathbf{x}_i)=\frac{1}{n-1}\|\mathbf{x}_i\|^2,$
• la covarianza è $cov(\mathbf{x}_i,\mathbf{x}_j)=\frac{1}{n-1}\langle \mathbf{x}_i, \mathbf{x}_j\rangle.$

Il nostro dataset si può dunque rappresentare con una matrice che ha per colonne i vettori delle features già centrati: \[X = \begin{bmatrix} x_{1,1}& x_{1,2} &\dots &x_{1,p} \\ x_{2,1}& x_{2,2} &\dots &x_{2,p} \\ .& . &. &. \\ .& . & \;\;. &. \\ .& . & \;\;\;\;. &. \\ x_{n,1}& x_{n,2} &\dots &x_{n,p} \end{bmatrix}\] La matrice di covarianza $C=(cov(\mathbf{x}_i,\mathbf{x}_j))$ è \[ C = \frac{1}{n-1} X^T X, \] ha dimensione $p\times p$, è simmetrica poiché $cov(\mathbf{x}_i,\mathbf{x}_j)=cov(\mathbf{x}_j,\mathbf{x}_i)$ e ha per diagonale le varianze $var(\mathbf{x}_i)=cov(\mathbf{x}_i,\mathbf{x}_i).$ Poiché $C$ è simmetrica e semi-definita positiva, ammette una base ortonormale di autovettori $\{\mathbf{u}_1, \mathbf{u}_2, \dots, \mathbf{u}_p\}$ con $\mathbf{u}_i\in\mathbb R^p$ quindi tali che \[ C \mathbf{u}_i = \lambda_i \mathbf{u}_i. \] In particolare $C$ ha una decomposizione spettrale \[C =𝑄Λ𝑄^T \] dove:

• $𝑄$ è una matrice ortogonale \(𝑄^T𝑄=𝐼\) le cui colonne sono autovettori ortonormali,
• $Λ$ è diagonale con autovalori in diagonale.

La PCA costruisce dunque una base ortonormale dello spazio delle variabili, non dello spazio delle osservazioni, i cui vettori base sono gli autovettori della matrice di covarianza ordinati per autovalori, ovvero varianza, decrescenti.
Le componenti principali dei vettori $\mathbf{x}_i$ \[ \mathbf{ξ}_i = X\mathbf{u}_i \] sono le coordinate dei dati lungo queste nuove direzioni.
Ciò ha per effetti pratici: l'eliminazione del rumore, la compressione dei dati, la visualizzazione (2D/3D).
Ad esempio: clustering più stabile, classificazione con meno overfitting, anomaly detection (outlier lontani dalle componenti principali).
Senza ortonormalità le componenti sarebbero correlate, si avrebbe informazione “doppia”

Consideriamo un esempio concreto e minimale in Python che evidenzia perché una base ortonormale è utile nel Data Mining, usando PCA su dati reali.
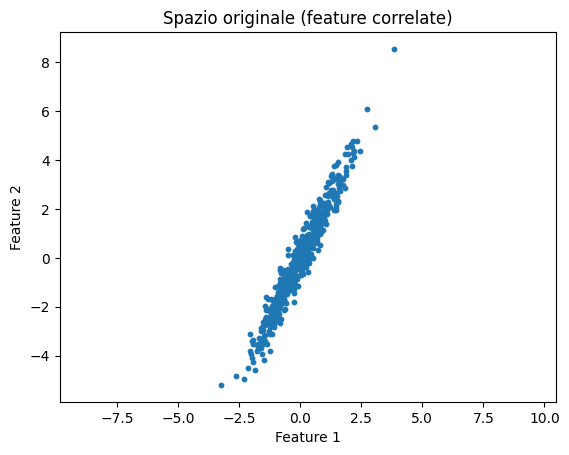
Useremo un dataset con feature correlate e faremo un confronto dopo il cambio di base ortonormale.

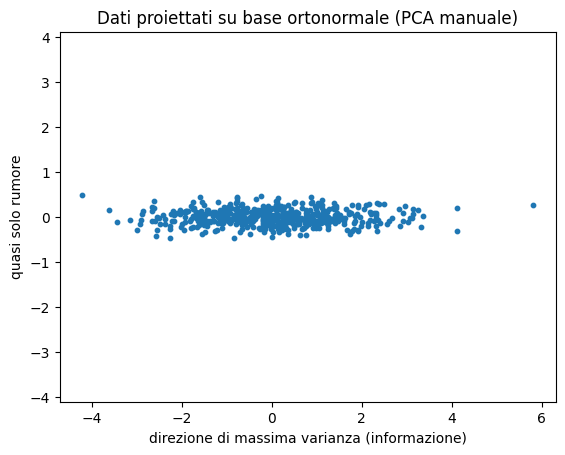
la PCA è diagonalizzazione ortogonale di 𝐶, gli autovettori sono direzioni di varianza massima, assi indipendenti per coordinate “naturali” dei dati.
Risultato tipico: clustering instabile nello spazio originale, clustering robusto nello spazio PCA dato che le distanze sono calcolate su assi indipendenti.
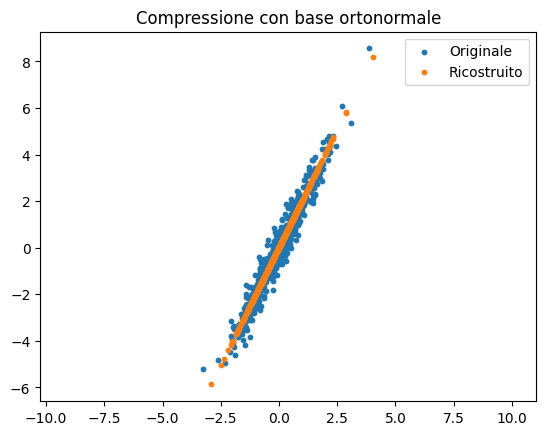
Si osserva che la struttura è preservata e il rumore è attenuato.

Quando il numero di variabili \(p\) è molto più grande del numero di osservazioni \(n\), caso estremamente importante in machine learning, genomica, elaborazione di immagini e Natural Language Processing, la PCA cambia natura in modo profondo.
La matrice di covarianza \(C\) ha almeno \(p - n\) autovalori nulli, è singolare, non è invertibile, non può avere più di \(n\) componenti principali non banali.
In alta dimensionalità, la PCA ha al massimo \(n\) componenti principali utili, anche se le variabili sono \(p\). Gli autovettori della covarianza sono in \(\mathbb{R}^p\), ma solo \(n\) sono significativi.
La decomposizione spettrale di \(C\): \[ C = Q \Lambda Q^\top \] produce \(p\) autovettori ortonormali in \(\mathbb{R}^p\) ma solo i primi \(n\) hanno autovalori non nulli, gli altri \(p-n\) sono direzioni “vuote”, senza varianza. Quindi non si ottiene una base utile di \(\mathbb{R}^p\) ma una base ortonormale dello spazio delle variabili con moltissime direzioni degeneri.
Dunque la PCA classica diventa inefficiente e numericamente instabile: calcolare \(X^\top X\) quando \(p\) è enorme costa molto, è numericamente instabile, produce una matrice gigantesca \(p \times p\) ma di rango massimo \(n\).
In alta dimensionalità si usa la Singular Value Decomposition (SVD) della matrice dei dati centrata: \[ X_c = U \Sigma V^\top. \] dove

• \(U \in \mathbb{R}^{n \times n}\) è una matrice unitaria complessa con colonne ortonormali,
• \(V \in \mathbb{R}^{p \times p}\) ha colonne ortonormali,
• \(\Sigma\in \mathbb{R}^{n \times p}\) è matrice rettangolare diagonale n×n con numeri reali non negativi sulla diagonale con \(n\) valori singolari non nulli.

Poiché \[ X^\top X = V \Sigma^2 V^\top. \] gli autovettori della covarianza sono le colonne di \(V\) e gli autovalori sono i quadrati dei valori singolari ma soprattutto si possono ottenere i primi \(n\) autovettori senza mai costruire \(X^\top X\).
In alta dimensionalità lo spazio delle osservazioni ha dimensione \(n\), quello delle variabili ha dimensione \(p\), ma i dati vivono in un sottospazio di dimensione al massimo \(n\).

La tecnica è usata in recommender systems (latent factors), topic modeling (LSA), text mining (TF-IDF + SVD).
Una interpretazione consiste nel considerare gli assi latenti come “concetti” indipendenti e ogni documento/utente è una combinazione ortogonale di essi.

Alcune applicazioni sono le seguenti.

• Negli anni '90, la PCA veniva usata per creare le "Eigenfaces". Un'immagine di un volto con 10.000 pixel veniva proiettata su una base ortonormale di "volti base". Bastavano poche decine di queste proiezioni (i coefficienti) per identificare una persona, riducendo drasticamente lo spazio di archiviazione e la velocità di confronto.
• Nei moderni modelli di linguaggio, le parole sono rappresentate in spazi vettoriali ad altissima dimensione. Per visualizzare come il modello "pensa" o per velocizzare i calcoli, si usano proiezioni ortogonali per ridurre queste dimensioni a poche centinaia, mantenendo le relazioni semantiche tra le parole.
• Molte tecniche di ottimizzazione delle reti neurali (come il Pruning o la Low-rank factorization) utilizzano la scomposizione in basi ortonormali per identificare quali pesi della rete sono meno "energetici" e possono essere rimossi senza che la capacità predittiva del modello ne risenta significativamente.

In sintesi, nell'AI, passare a una base ortonormale ottimale significa cambiare punto di vista per vedere il dataset nella sua forma più semplice. L'identità di Parseval ci dà il "budget" dell'informazione, permettendoci di sapere con precisione quanto stiamo semplificando la realtà senza perderne l'essenza.