Teoria Spettrale

La teoria spettrale, delle basi ortonormali adattate agli operatori, nasce dall’idea di generalizzare la diagonalizzazione delle matrici simmetriche agli operatori lineari su spazi di Hilbert.
In dimensione finita una matrice simmetrica \(A\) ha una base ortonormale di autovettori, e si scrive \[ A = Q \Lambda Q^\top \] dove \(Q\) è la matrice le cui colonne sono gli autovettori normalizzati (ortonormali) di \(A\) e poiché \(Q\) è ortogonale \(Q^{\top }=Q^{-1}\) e \(Q^{\top }Q=I\). Inoltre \(\Lambda \) è matrice diagonale degli autovalori \(\lambda _{i}\) di \(A\).

La versione infinito-dimensionale per un operatore autoaggiunto limitato \(T\) è: \[T = \sum_n \lambda |e_n\rangle\langle e_n| \]

Le basi ortonormali sono il linguaggio naturale della teoria spettrale per tre motivi fondamentali.

Se \(\{e_n\}\) è una base ortonormale di autovettori di \(T\), \[ T e_n = \lambda_n e_n, \] ogni \( f \in \mathcal H\) si espande come \[ f = \sum_n \langle f, e_n\rangle e_n \] e in questa base: \[ Tf = \sum_n \lambda_n \langle f, e_n\rangle e_n, \] cioè \(T\) agisce moltiplicando le coordinate e questo è il modo più semplice possibile di descrivere un operatore.
Le basi ortonormali rendono possibile definire funzioni di operatori.
Se \(T\) è diagonalizzabile in una base ortonormale \(\{e_n\}\), allora: \[ f(T) = \sum_n f(\lambda_n) \, \langle \cdot, e_n\rangle e_n \quad \forall f\in \mathcal H. \] Questo è fondamentale per risolvere equazioni differenziali, definire \(e^{tT}\) (semigruppi), definire radici, potenze, inversi.
Permettono inoltre di decomporre lo spazio in sottospazi invarianti. La decomposizione spettrale divide \(H\) in sottospazi associati a singoli autovalori, sottospazi continui, sottospazi residui. Ognuno è generato da una famiglia ortonormale. È l’analogo infinito-dimensionale della decomposizione in autospazi.

La teoria spettrale dunque studia gli operatori lineari attraverso i loro autovalori e autovettori, basi ortonormali che sono lo strumento fondamentale per diagonalizzarli, definire funzioni di operatori, decomporre lo spazio in parti indipendenti, rendendo “trasparenti” e manipolabili gli operatori.

Teorema spettrale
Ogni operatore autoaggiunto su uno spazio di Hilbert è un “integrale” di proiezioni ortogonali.

In forma astratta: \[ T = \int_{\sigma(T)} \lambda \, dE_\lambda. \] In forma concreta, se esiste una base ortonormale di autovettori \(\{e_n\}_{n\in\mathbb N}:\) \[ T = \sum_n \lambda_n P_n, \] dove \(P_n\) è la proiezione ortogonale sul sottospazio generato da \(e_n\). Le proiezioni ortogonali sono gli “atomi” della teoria spettrale.

Seguono alcuni esempi che mostrano il ruolo delle basi ortonormali.

Fourier
La base ortonormale \(\{e^{inx}\}\) diagonalizza
- l’operatore derivata \[ \frac{d}{dx} e^{inx} = in e^{inx}. \]
- l’operatore laplaciano: \[ -\frac{d^2}{dx^2} e^{inx} = n^2 e^{inx}. \]
Hermite
La base degli Hermite diagonalizza l’oscillatore armonico \(H = -\frac{d^2}{dx^2} +x^2\): \[ H\psi_n = (2n+1)\psi_n. \]

che considerando la relazione \(H_n(x)=2xH_{n-1}(x)-2(n-1)H_{n-2}(x)\) vale zero.
Laguerre
La base dei Laguerre diagonalizza l’operatore radiale dell’idrogeno.
Legendre
La base dei Legendre diagonalizza l’operatore di Laplace sulla sfera.

In tutti questi casi, la base ortonormale trasforma un operatore complicato in un operatore semplice.

Un esempio numerico è la diagonalizzazione spettrale del Laplaciano 1D discreto con condizioni di Dirichlet. L’operatore discreto (matrice) \(A \in \mathbb{R}^{n\times n}\): \[ A = \frac{1}{h^2} \begin{pmatrix} -2 & 1 & 0 & \cdots & 0 \\ 1 & -2 & 1 & \ddots & \vdots \\ 0 & 1 & -2 & \ddots & 0 \\ \vdots & \ddots & \ddots & \ddots & 1 \\ 0 & \cdots & 0 & 1 & -2 \end{pmatrix}, \quad h = \frac{1}{n+1}. \] È l’analogo discreto di \(-u''\) su \((0,1)\) con \(u(0)=u(1)=0\). Gli autovettori sono discretizzazioni di \(\sin(k\pi x)\), e formano una base ortonormale; gli autovalori approssimano \((k\pi)^2\).

# ---------------- Parametri ----------------
n = 50                 # numero di punti interni
h = 1.0 / (n + 1)      # passo spaziale
x = np.linspace(h, 1.0 - h, n)  # punti interni (0,1)

# ---------------- Matrice Laplaciano discreto ----------------
# A u ≈ -u'' con condizioni di Dirichlet
diag = -2.0 * np.ones(n)
off  =  1.0 * np.ones(n-1)
A = (np.diag(diag) + np.diag(off, 1) + np.diag(off, -1)) / (h**2)

# ---------------- Diagonalizzazione spettrale ----------------
# A è simmetrica reale -> uso eigh
evals, evecs = np.linalg.eigh(A)

# ordino per autovalore crescente
idx = np.argsort(evals)
evals = evals[idx]
evecs = evecs[:, idx]

# ---------------- Verifica ortonormalità ----------------
G = evecs.T @ evecs
print("Deviazione da identità (||Q^T Q - I||):", np.linalg.norm(G - np.eye(n)))

# ---------------- Confronto con autovalori teorici ----------------
k = np.arange(1, n+1)
lambda_theory = (k * np.pi)**2

print("\nPrimi 5 autovalori numerici vs teorici:")
for j in range(5):
    print(f"k={j+1}: num={evals[j]:.6f}, teorico≈{lambda_theory[j]:.6f}")

# ---------------- Grafico: primi autovettori ----------------
plt.figure(figsize=(10, 6))
for j in range(3):
    plt.plot(x, evecs[:, j], label=f"autovettore {j+1} (λ≈{evals[j]:.2f})")
plt.xlabel("x")
plt.ylabel("valore")
plt.title("Primi autovettori del Laplaciano discreto (base ortonormale)")
plt.grid(True)
plt.legend()

# ---------------- Azione diagonale in base spettrale ----------------
# prendo una funzione f(x) = x(1-x) e la proietto sulla base degli autovettori
f = x * (1 - x)
coeff = evecs.T @ f          # coordinate spettrali
Af_direct = A @ f            # applicazione diretta
Af_spectral = evecs @ (evals * coeff)  # A f = Q Λ Q^T f

print("\nErrore tra A f (diretto) e A f (spettrale):",
      np.linalg.norm(Af_direct - Af_spectral))

# grafico di f e della ricostruzione spettrale (usando tutti i modi)
plt.figure(figsize=(10, 6))
plt.plot(x, f, 'k', lw=2, label="f(x) = x(1-x)")
plt.plot(x, Af_direct, 'r--', lw=1.5, label="A f (diretto)")
plt.plot(x, Af_spectral, 'b:', lw=1.5, label="A f (via base spettrale)")
plt.xlabel("x")
plt.ylabel("valore")
plt.title("Azione di A su f: confronto diretto vs spettrale")
plt.grid(True)
plt.legend()

plt.show()

Deviazione da identità (||Q^T Q - I||): 1.0733667317925748e-14

Primi 5 autovalori numerici vs teorici:
k=1: num=-10394.133516, teorico≈9.869604
k=2: num=-10364.571491, teorico≈39.478418
k=3: num=-10315.426065, teorico≈88.826440
k=4: num=-10246.883661, teorico≈157.913670
k=5: num=-10159.204286, teorico≈246.740110

Errore tra A f (diretto) e A f (spettrale): 7.167008484371411e-12

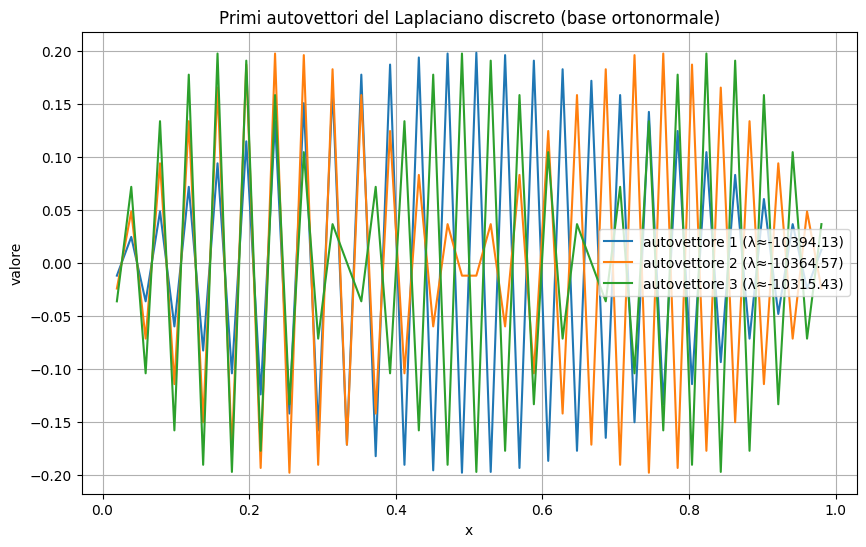
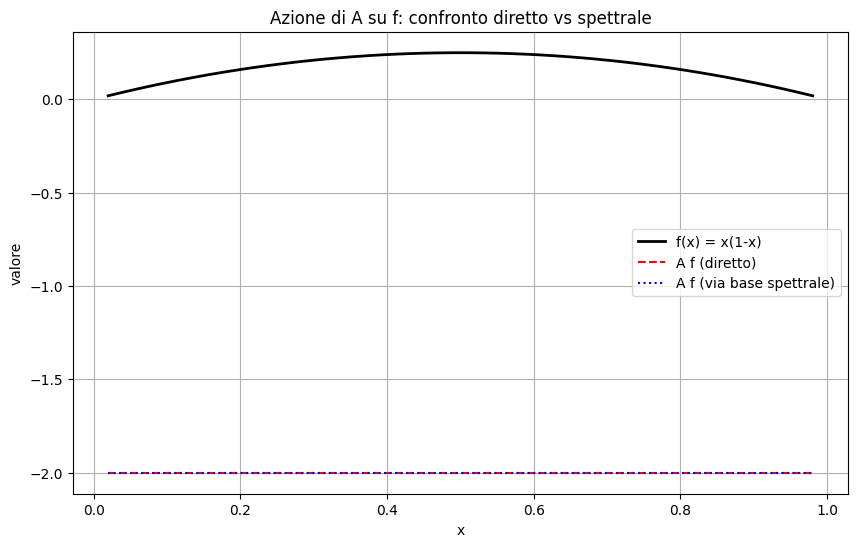
Questo esempio mostra

gli autovettori di \(A\) formano una base ortonormale numerica: \(Q^T Q \approx I\);
in questa base, \(A\) è diagonale: \(A = Q \Lambda Q^T\)
applicare \(A\) a una funzione \(f\) è equivalente a:
1. proiettare \(f\) sulla base ortonormale (coeff spettrali),
2. moltiplicare ogni coefficiente per l’autovalore corrispondente,
3. ricombinare gli autovettori.

È esattamente la filosofia della teoria spettrale: una base ortonormale adattata all’operatore rende l’operatore trasparente.

Bibliografia

Spectral theory, From Wikipedia, the free encyclopedia

❮❮ ❯❯