Trasformata di Fourier
La trasformata di Fourier è uno degli strumenti più potenti dell’analisi matematica. In fisica, ingegneria, teoria dei segnali, probabilità, PDE, quantistica: ovunque compaia un fenomeno oscillatorio, la trasformata di Fourier è la lente che permette di leggerlo.
Nello spazio di Hilbert \(L^2(\mathbb{R})\) che essa rivela la sua forma più elegante e profonda. La trasformata di Fourier è, in fondo, un cambio di base ortonormale che rende trasparenti gli operatori differenziali e così permette di risolvere PDE, analizzare segnali, comprendere fenomeni fisici e probabilistici.
La trasformata di Fourier di una funzione \(f\in L^1\cap L^2\) è: \[ \hat f(\xi) = \int_{-\infty}^{\infty} f(x)e^{-2\pi i x\xi}\,dx. \] Le funzioni \(e^{2\pi i x\xi}\) sono onde pure, e formano una base ortonormale generalizzata di \(L^2\). La trasformata di Fourier non fa altro che esprimere \(f\) come combinazione di queste onde: \[ f(x) = \int_{-\infty}^{\infty} \hat f(\xi) e^{2\pi i x\xi}\, d\xi. \] È una decomposizione spettrale: la frequenza \(\xi\) è l’autovalore, l’onda \(e^{2\pi i x\xi}\) è l’autovettore.
Passaggio cruciale è ilLa trasformata di Fourier si estende in modo unico a un operatore unitario \[ \mathcal{F}: L^2(\mathbb{R}) \to L^2(\mathbb{R}), \] preservando la norma: \[ \|\hat f\|_{L^2} = \|f\|_{L^2}. \]
La derivata è un operatore differenziale: \[ D = \frac{d}{dx}. \] In \(L^2\), la trasformata di Fourier lo diagonalizza: \[ \mathcal{F}(Df)(\xi) = (2\pi i \xi)\hat f(\xi). \] Questo è il cuore della teoria spettrale:
- \(D\), a meno di dettagli tecnici sul dominio, è un operatore autoaggiunto,
- le onde \(e^{2\pi i x\xi}\) sono le sue autofunzioni,
- la trasformata di Fourier è la mappa che porta \(D\) in un operatore di moltiplicazione.
Dunque le proprietà fondamentali della trasformata di Fourier in \(L^2\), alla base dell’analisi dei segnali, della fisica quantistica e delle PDE sono elencabili come nel seguito.
- Unitarietà \[ \|f\|_{L^2} = \|\hat f\|_{L^2}. \]
- Invertibilità \[ f(x) = \int_{-\infty}^{\infty} \hat f(\xi)e^{2\pi i x\xi}\,d\xi. \]
- Trasforma la convoluzione nella moltiplicazione \[ \widehat{f*g} = \hat f \cdot \hat g. \]
- Trasforma la derivazione in moltiplicazione per \(\xi\) \[ \widehat{f'}(\xi) = 2\pi i \xi \hat f(\xi). \]
- Trasforma una traslazione in uno sfasamento \[ \widehat{f(x-a)} = e^{-2\pi i a\xi}\hat f(\xi). \]
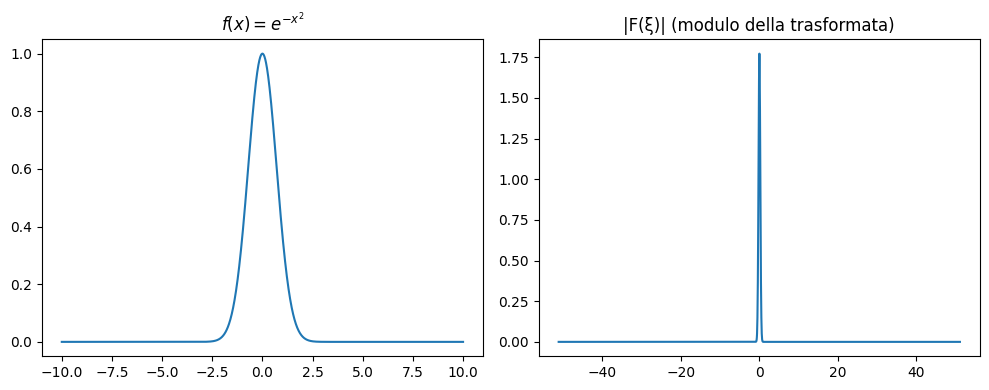
L'esempio seguente mostra un caso emblematico della simmetria profonda della trasformata: la trasformata di Fourier di una gaussiana è ancora una gaussiana.
# dominio
x = np.linspace(-10, 10, 2048)
dx = x[1] - x[0]
# funzione: gaussiana
f = np.exp(-x**2)
# trasformata numerica (FFT)
F = np.fft.fftshift(np.fft.fft(np.fft.ifftshift(f))) * dx
xi = np.fft.fftshift(np.fft.fftfreq(len(x), d=dx))
plt.figure(figsize=(10,4))
plt.subplot(1,2,1)
plt.plot(x, f)
plt.title("f(x) = e^{-x^2}")
plt.subplot(1,2,2)
plt.plot(xi, np.abs(F))
plt.title("|F(ξ)| (modulo della trasformata)")
plt.tight_layout()
plt.show()
 Con la libreria sympy.
Con la libreria sympy.
s, t = symbols('s t')
fourier_transform(exp(-t**2), t, -s)
\(\sqrt{\pi} e^{- \pi^{2} s^{2}}\)
inverse_fourier_transform(sqrt(pi)*exp(-(pi*s)**2), s, t)
\(e^{- t^2}\)
La trasformata di Fourier in \(L^2\), uno dei ponti più profondi tra matematica pura e applicata, unisce:
- analisi funzionale (operatori unitari, spettri, basi ortonormali),
- PDE (diagonalizzazione della derivata e del Laplaciano),
- fisica quantistica (momento ↔ frequenza),
- teoria dei segnali (filtri, convoluzioni, spettro),
- probabilità (caratteristiche, gaussiane, processi stocastici),
- metodi numerici (FFT, spettrali, Galerkin).
Cugine della trasformata di Fourier sono le seguenti
- Trasformata di Laplace
nello spazio funzionale \(L^2([0,\infty[, e^{-2ax}dx)\) o funzioni di crescita controllata diagonalizza l’operatore derivata su funzioni causali: \[ \mathcal{L}(f')(s) = s \mathcal{L}(f)(s) - f(0). \] “sposta” la derivata in una moltiplicazione esattamente come Fourier, ma adattata al semiasse positivo.
Strumento principe per: - risolvere equazioni differenziali ordinarie lineari - analizzare sistemi dinamici e controllo - studiare stabilità (poli e zeri) - trattare funzioni causali (segnali che iniziano a \(t=0\)) - risolvere PDE paraboliche e iperboliche tramite separazione si applica - circuiti elettrici - sistemi lineari tempo-invarianti - teoria del controllo - PDE (calore, onde, diffusione) - probabilità (tempi di attesa, distribuzioni esponenziali) - Trasformata di Mellin
Nello spazio funzionale \(L^2(]0,\infty[, x^{2c-1}dx)\) diagonalizza operatori di dilatazione: \[ f(x) \mapsto f(ax). \] È l’analogo della trasformata di Fourier, ma per la simmetria moltiplicativa invece che additiva, trasforma prodotti in convoluzioni e viceversa, ma nel senso “moltiplicativo”: \[ \mathcal{M}(f(ax)) = a^{-s} \mathcal{M}(f)(s). \] È fondamentale quando la variabile naturale è logaritmica e le sue applicazioni chiave sono:- analisi asintotica (metodo di Watson, Tauberiani)
- teoria dei numeri (funzione zeta, Dirichlet)
- equazioni integrali su domini non compatti
- computer vision (invarianti di scala)
- problemi con simmetria di scala (turbulenza, frattali)
- Trasformata di Hankel
Nello spazio funzionale: \(L^2(]0,\infty[, r\,dr)\) o varianti è la versione radiale della trasformata di Fourier. Se una funzione è radiale \(f(x)=g(|x|)\), allora: \[ \widehat{f}(\xi) = \mathcal{H}_\nu(g)(|\xi|), \] dove \(\nu = \frac{n}{2}-1\). La Hankel diagonalizza l’operatore di Bessel: \[ r^2 f'' + r f' + (r^2 - \nu^2) f = 0. \] È la trasformata naturale per problemi con simmetria circolare o sferica con applicazioni chiave:- equazioni di Helmholtz e Laplace in domini radiali
- scattering ondoso
- ottica e diffrazione
- segnali radiali (MRI, radar)
- PDE in coordinate cilindriche o sferiche
| Trasformata | Simmetria | Operatore diagonalizzato | Dominio naturale | Applicazioni |
| Fourier | traslazioni | derivata | \(\mathbb{R}\) | segnali, PDE, quantistica |
| Laplace | causalità + traslazioni | derivata (causale) | \([0,\infty[\) | ODE, sistemi, controllo |
| Mellin | scalatura | operatore di dilatazione | \(]0,\infty[\) | analisi asintotica, numeri |
| Hankel | rotazioni | operatore di Bessel | funzioni radiali | PDE radiali, fisica |
- sono operatori unitari (in spazi di Hilbert appropriati),
- diagonalizzano operatori differenziali fondamentali,
- permettono di risolvere PDE tramite moltiplicazione in frequenza,
- forniscono basi ortonormali o integrali spettrali,
- rivelano la struttura profonda degli spazi funzionali.