Poliamanti
Esaminiamo un altro esempio di poliforme oltre ai polimini.
Il termine "poliamante" (polydiamond) fu coniato dal matematico T.H. O'Beirne. Il nome deriva dalla forma, a "diamante", creata da due triangoli equilateri adiacenti.
La visualizzazione delle celle di una griglia di triangoli equilateri in Python presenta qualche difficoltà in più rispetto a una griglia quadrata.
import matplotlib.patches as patches
def plot_Poliamante(S):
fig, ax = plt.subplots()
ax.set_aspect('equal')
for (x, y) in S:
if y % 2 == 0:
x0 = x - (y -y//2) / 2
y0 = (y +y//2) * np.sqrt(3) / 6
vertices = [
(x0 - 1 / 2, y0 - np.sqrt(3) / 6),
(x0 + 1 / 2, y0 - np.sqrt(3) / 6),
(x0 , y0 + np.sqrt(3) / 3)]
else:
x0 = x - (y -(y-1)//2)/ 2
y0 =(y +(y-1)//2) * np.sqrt(3) / 6
vertices = [
(x0, y0 - np.sqrt(3) / 3),
(x0 - 1 / 2, y0 + np.sqrt(3) / 6),
(x0 + 1 / 2, y0 + np.sqrt(3) / 6)]
triangle = patches.Polygon(vertices, closed=True, facecolor='lightblue',edgecolor='black', linewidth=1)
ax.add_patch(triangle)
ax.text(x0,y0, f"{x},{y}",horizontalalignment='center')
plt.axis('off')
ax.set_xlim(min(x for x,_ in S)-1, max(x for x,_ in S)+1)
ax.set_ylim(min(y for _,y in S)-1, max(y for _,y in S)+1)
# Impostazione tick interi per entrambi gli assi
ax.set_xticks(range(min(x for x,_ in S)-1, max(x for x,_y in S)+1))
ax.set_yticks(range(min(y for _,y in S)-1, max(y for _,y in S)+1))
plt.show()
plot_Poliamante({(-1,0),(-1,-1),(0,-1),(0,1),(1,1),(2,0)})
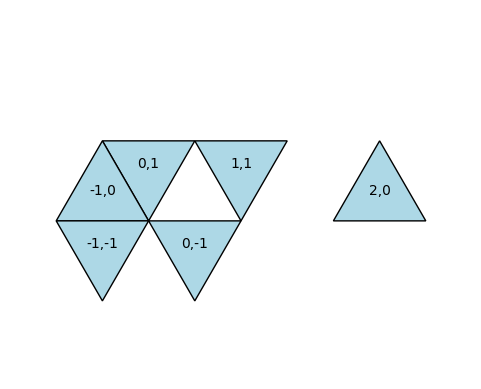
Analoga difficoltà si ritrova nella generazione casuale di un insieme connesso di triangoli equilateri, una forma di poliamanti, di un numero dato di elementi a partire da un primo triangolo.
def generaPoliam(n):
S = {(0,0)}
B = {(1,1), (0,1), (0,-1)}
for i in range(n-1):
(x,y) = random.choice(tuple(B))
S.add((x,y))
B.remove((x,y))
if y%2 == 0:
B = B | {(x,y-1), (x,y+1), (x+1,y+1)} - S
else:
B = B | {(x,y-1), (x,y+1), (x-1,y-1)} - S
return S, B
S, B = generaPoliam(10)
plot_Poliamante(S), plot_Poliamante(B)
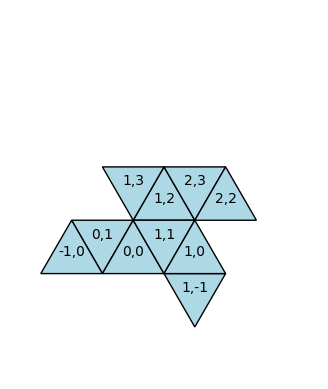
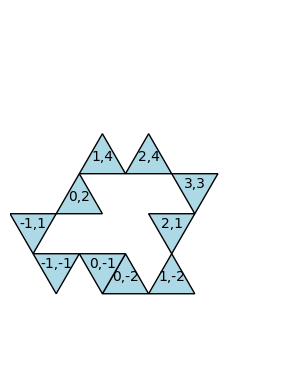
Per approfondimenti:
- Polyiamond, From Wikipedia, the free encyclopedia