La bellezza matematica dei polimini risiede nella loro capacità di generare complessità infinita da regole semplici, offrendo un microcosmo dove esplorare i principi fondamentali della forma e della struttura. La classificazione morfologica dei polimini rappresenta un ponte tra matematica pura e applicata. L'analisi di indicatori quantitativi e qualitativi consente di categorizzare queste strutture discrete secondo caratteristiche geometriche fondamentali.

Il rapporto tra perimetro e area di un polimino, il suo numero di elementi $n$, è un indicatore semplice ma informativo per una classificazione morfologica: misura la compattezza della forma, tra un valore minimo $\frac{4\sqrt n}{n}$ per le forme quadrate a $\frac{2n+2}{n}$ per le forme a asta, assumendo valori massimi per forme a "T", "X" o strutture dendritiche.
Altri semplici indicatori sono:

• il rapporto tra altezza massima e larghezza massima (aspect ratio) per l'allungamento direzionale;
  def aspect_ratio(S): lst_x, lst_y = zip(*S) width = max(lst_x) - min(lst_x) + 1 height = max(lst_y) - min(lst_y) + 1 return height/width
• il rapporto tra l'area del polimino e quella del più piccolo rettangolo che lo contiene;
  def A_R(S): lst_x, lst_y = zip(*S) width = max(lst_x) - min(lst_x) + 1 height = max(lst_y) - min(lst_y) + 1 return len(S)/(width*height)
• il rapporto tra l'area del polimino e la lunghezza della diagonale del più piccolo rettangolo che lo contiene;
  def A_Rdiag(S): lst_x, lst_y = zip(*S) width = max(lst_x) - min(lst_x) + 1 height = max(lst_y) - min(lst_y) + 1 return len(S)/np.sqrt(width**2 + height**2)
• l'indice di ramificazione, ovvero il rapporto tra il numero di vertici grado 3 o 4 e il numero totale di vertici;
  def vertici_molt(S): count = dict() for (x, y) in S: for v in {(x, y), (x+1, y), (x, y+1), (x+1, y+1)}: count[v] = 1 if v not in count else count[v]+1 return count def n_vertici_molt(S,k): count = vertici_molt(S) return len({v for v, c in count.items() if c == k})
  ​
• il rapporto tra l'area del bordo esterno, o del bordo interno o dell'interno, e quella del polimino oppure il rapporto tra l'area del bordo esterno e quella del bordo interno.

Un indicatore più sofisticato, è il raggio di girazione definito come: \[ R_g = \sqrt{\frac{1}{n} \sum_{i=1}^n \|\mathbf{r}_i - \mathbf{r}_0\|^2} \] dove $\mathbf{r}_0$ è il centro di massa.

I precedenti indicatori possono essere valutati in una pagina dinamica interattiva insieme ad altri più complessi come i seguenti:

• i momenti di inerzia che misurano come la "massa", cioè le celle, è distribuita rispetto agli assi;
  def Inerzia(S): r = np.array(list(S)) x_CM, y_CM = np.mean(r, axis=0) # centro di massa I_xx = np.sum((r[:, 0] - y_CM)**2) # Rispetto asse x I_yy = np.sum((r[:, 1] - x_CM)**2) # Rispetto asse y I_xy = -np.sum((r[:, 0] - x_CM) * (r[:, 1] - y_CM)) # Prodotto di inerzia return I_xx, I_yy, I_xy
• l'anisotropia, il grado di direzionalità/allungamento, se minore di 0.1 indica forma circolare, maggiore di 1 indica forma allungata;
  def anisotropia(S): I_xx, I_yy, _ = Inerzia(S) # Anisotropia (0 = isotropo, 1 = massima anisotropia) return abs(I_xx - I_yy) / (I_xx + I_yy) if (I_xx + I_yy) > 0 else 0
• la direzione di massima estensione e la direzione di minima estensione, ortogonali tra loro;
  def direz(S): I_xx, I_yy, I_xy = Inerzia(S) I = np.array([ [I_xx, I_xy], [I_xy, I_yy] ]) eigenvalues, eigenvectors = np.linalg.eigh(I) return { 'Imin': eigenvalues[0], # Momento principale minore 'Imax': eigenvalues[1], # Momento principale maggiore 'Imax/Imin': eigenvalues[1]/eigenvalues[0], # Rapporto di allungamento 'axis1': eigenvectors[:, 0], # Direzione primo asse principale 'axis2': eigenvectors[:, 1] # Direzione secondo asse principale }
• il grado di simmetria rispetto a una cella o rispetto a linee di celle parallele agli assi coordinati;
  def gradoSimmC(S,C): lstx, lsty = zip(*S) x_C, y_C = C lstx, lsty = [2*x_C-x for x in lstx], [2*y_C-y for y in lsty] S1 = set(zip(lstx, lsty)) return len(S & S1)/len(S) def gradoSimmAss(S,asse,C): lstx, lsty = zip(*S) x_C, y_C = C if asse == 'y': lstx = [2*x_C-x for x in lstx] else: lsty = [2*y_C-y for y in lsty] S1 = set(zip(lstx, lsty)) return len(S & S1)/len(S)
• il numero di concavità, ovvero il numero di "rientranze" nel contorno; si potrebbe determinare come il numero di componenti connesse del complementare del polimino rispetto al rettangolo che ne è l'involucro;
  def Cbox(S): lst_x,lst_y = zip(*S) xM, xm = max(lst_x), min(lst_x) yM, ym = max(lst_y), min(lst_y) return {(x, y) for x in range(xm, xM + 1) for y in range(ym, yM + 1) if (x,y) not in S} def connected_components(S): visited = set() components = [] def dfs(s, comp): stack = [s] while stack: x, y = stack.pop() if (x, y) in visited: continue visited.add((x, y)) comp.add((x, y)) for (x,y) in [(x+1,y), (x-1,y), (x,y+1), (x,y-1)]: if (x,y) in S and (x,y) not in visited: stack.append((x,y)) for s in S: if s not in visited: comp = set() dfs(s, comp) components.append(comp) return components len([Si for Si in connected_components(Cbox(S))])
• il numero di "buchi"; ad esempio considerando quelle componenti connesse del complementare del polimino rispetto al polimino che ne è l'involucro convesso, o anche del rettangolo minimo che lo contiene, il cui bordo esterno è parte del polimino, con ciò considerando come buchi anche le "insenature" o rientranze inaccessibili;
  len([Si for Si in connected_components(invConv(S)-S) if bordoEst(Si).issubset(S)])
• la massima distanza tra due celle del polimino considerando:
  • la massima distanza euclidea;
    def max_dist_euclid(S): S = list(S) maxd = 0 coppia = None for i in range(len(S)): x1, y1 = S[i] for j in range(i+1, len(S)): x2, y2 = S[j] d = ((x1 - x2)**2 + (y1 - y2)**2)**0.5 if d > maxd: maxd = d coppia = (S[i], S[j]) return maxd, coppia
  • la massima distanza rispetto a $d((x_1,y_1),(x_2,y_2))=|x_2-x_1|+|y_2-y_1|$;
    def max_dist_manhattan(S): S = list(S) maxd = 0 coppia = None for i in range(len(S)): x1, y1 = S[i] for j in range(i+1, len(cells)): x2, y2 = S[j] d = abs(x1 - x2) + abs(y1 - y2) if d > maxd: maxd = d coppia = (S[i], S[j]) return maxd, coppia
  • la distanza massima in “passi ortogonali” (come BFS all’interno del polimino), vero diametro topologico del polimino.
    def max_geodesic_distance(S): # BFS per trovare il punto più distante da un qualunque punto def bfs(start): visited = {start: 0} queue = deque([start]) farthest = (start, 0) while queue: xc,yc = queue.popleft() for (x,y) in {(xc+1,yc),(xc,yc+1),(xc-1,yc),(xc,yc-1)} & S: if (x,y) not in visited: visited[(x,y)] = visited[(xc,yc)] + 1 queue.append((x,y)) if visited[(x,y)] > farthest[1]: farthest = ((x,y), visited[(x,y)]) return farthest # Step 1: prendi una cella a caso start = next(iter(S)) a, _ = bfs(start) # Step 2: BFS da quella cella per trovare la distanza massima effettiva b, dist = bfs(a) return dist, (a, b)

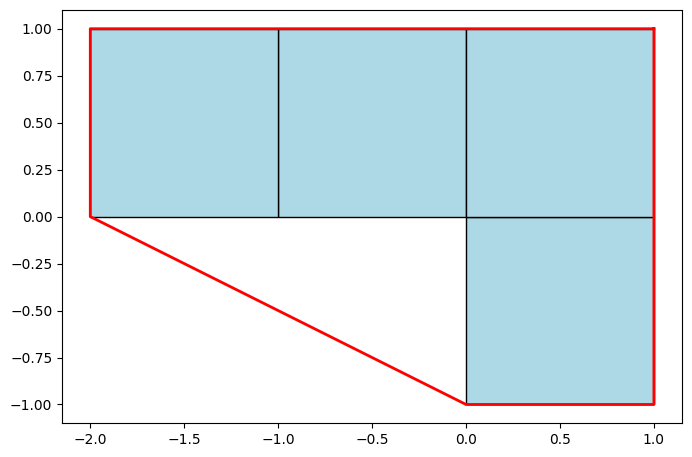
Infine possiamo considerare il rapporto tra area del polimino e area del suo involucro convesso che indica la convessità del polimino. Il metodo .ConvexHull() della libreria scipy.spatial fornisce le coordinate del poligono involucro (hull) convesso di un insieme di punti.

• POLYOMINOES, by Gill Barequet, Solomon W. Golomb, and David A. Klarner