Formalmente, un polimino è una delle forme assunte da un insieme connesso di celle sul reticolo quadrato, cioè un insieme in cui ogni coppia di celle è collegata da un percorso di celle dell'insieme in cui ciascuna condivide un lato con la seguente. La loro forma può considerarsi come ciò che non varia per traslazione (fixed), per traslazione e rotazione (one-sided) o per traslazione, rotazione e simmetrie (free).
| numero di quadrati | nome | free | one-sided | fixed |
|---|---|---|---|---|
| 1 | monomino | 1 | 1 | 1 |
| 2 | domino | 1 | 1 | 2 |
| 3 | trimino | 2 | 2 | 6 |
| 4 | tetramino | 5 | 7 | 19 |
| 5 | pentamino | 12 | 18 | 63 |
| 6 | esamino | 35 | 60 | 216 |
| 7 | eptamino | 108 | 160 | 760 |
| 8 | ottamino | 369 | 704 | 2725 |
| 9 | ennamino | 1285 | 2500 | 9910 |
| 10 | decamino | 4655 | 9189 | 36446 |
| ... | ... | ... | ... | ... |
Possiamo verificare se un insieme di celle forma un polimino utilizzando due fondamentali strategie per esplorare grafi: un algoritmo BFS (Breadth-First Search) di ricerca in ampiezza, che visita i nodi livello per livello, partendo dal nodo sorgente, e un algoritmo DFS (Depth-First Search) di ricerca in profondità, che esplora il percorso più lungo possibile prima di tornare indietro.
Ad esempio possiamo procedere nel modo seguente.
def is_polimino(S):
visited = set()
stack = [lstS[0]]
while stack:
(x,y) = stack.pop()
if (x,y) not in visited:
visited.add((x,y))
for v in {(x+1,y), (x-1,y), (x,y+1), (x,y-1)} & S - visited:
stack.append(v)
return len(visited) == len(S)
is_polimino({(-1,0),(-1,-1),(0,1),(1,1),(2,0)})
False
is_polimino({(-1,0),(-1,-1)})
True
S = {(-1,2), (-1,1), (0,1), (0,2), (0,0), (1,1), (1,2), (0,3)}
is_polimino(S), is_polimino(interno(S)), is_polimino(S-interno(S)), is_polimino(bordo(S)), plot_S(S)
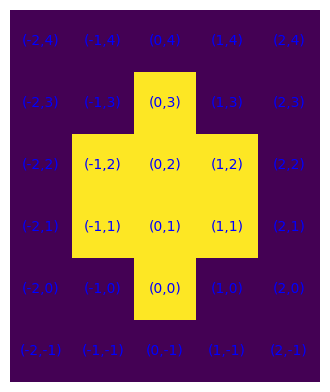
(True, True, False, False, None)
Possiamo cercare quali celle, rimosse, disconnettono l'insieme ovvero gli fanno perdere la forma di polimino. Sono dette punti di articolazione.
def ele_diArt(S):
A = set()
for s in S:
if not is_polimino(S-{s}):
A.add(s)
return A
plot_S(ele_diArt(S))
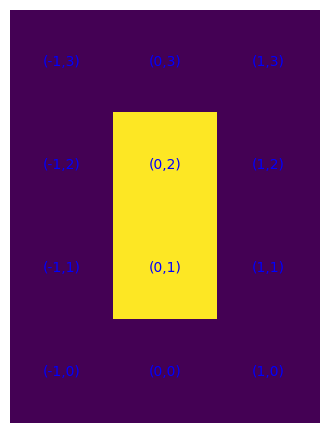
Per ottenere tutti i polimini (free) di un certo numero di elementi possiamo procedere come nel modo seguente.
from itertools import groupby, chain
from operator import itemgetter
from sys import argv
def concat_map(func, it):
return list(chain.from_iterable(map(func, it)))
def trasf(S):
"""Determina le varie trasformazioni piane dell'insieme di coordinate S."""
return (S,
[(y,-x) for (x,y) in S],
[(-x,-y) for (x,y) in S],
[(-y,x) for (x,y) in S],
[(-x,y) for (x,y) in S],
[(-y,-x) for (x,y) in S],
[(x,-y) for (x,y) in S],
[(y,x) for (x,y) in S])
def translate_to_O(S):
minx, miny = min(s[0] for s in S), min(s[1] for s in S)
return [(x - minx, y - miny) for (x, y) in S]
def canonical(S):
return min(sorted(translate_to_O(tS)) for tS in trasf(S))
def unique(lst):
lst.sort()
return list(map(next, map(itemgetter(1), groupby(lst))))
def new_pols(S):
"""Trova tutte le coordinate dei quadrati che possono essere aggiunte al polimino."""
# I quattro punti del vicinato secondo Von Neumann.
contiguous = lambda s: [(s[0] - 1, s[1]), (s[0] + 1, s[1]), (s[0], s[1] - 1), (s[0], s[1] + 1)]
new_points = unique([s for s in concat_map(contiguous, S) if s not in S])
return unique([canonical(S + [s]) for s in new_points])
def genPol(n):
"""Genera ricorsivamente tutti i polimini di n elementi."""
assert n >= 0
if n == 0: return []
if n == 1: return [[(0, 0)]]
return unique(concat_map(new_pols, genPol(n - 1)))
n = 4
lst_S = []
for i,P in enumerate(genPol(n)):
lst_S.append({(x +i*n, y) for (x, y) in P})
plot_S(*lst_S)
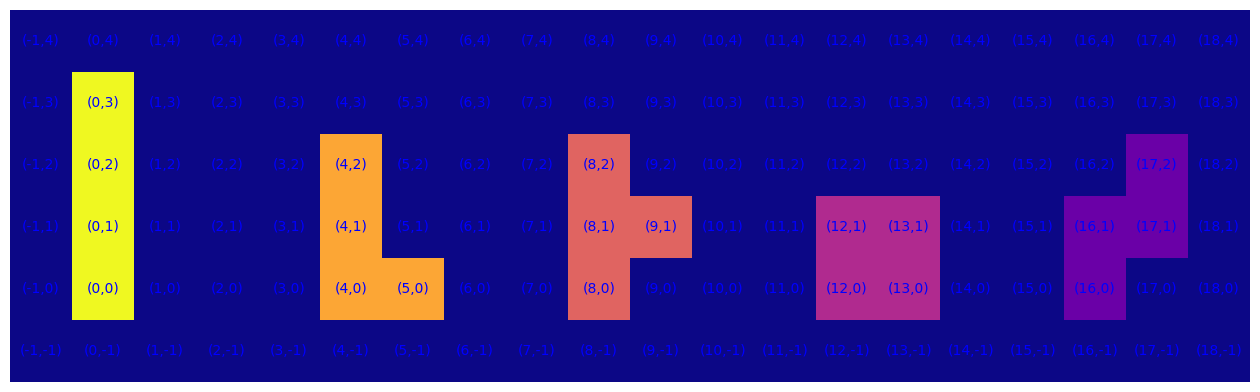
- POLYOMINOES, by Gill Barequet, Solomon W. Golomb, and David A. Klarner
- Free polyominoes enumeration, by Rosetta Code