Percorso minimo
Per trovare il percorso di minima lunghezza tra due celle di un insieme connesso possiamo usare il procedimento seguente con algoritmo BFS (Breadth-First Search) di ricerca in ampiezza, che visita i nodi livello per livello, partendo da una prima cella: esplora prima tutte le celle a distanza 1, poi distanza 2, ecc., come un'onda che si espande in uno stagno dopo un sasso. Si utilizza la struttura dati coda (queue), FIFO (First-In-First-Out), per memorizzare l'insieme delle celle visitate ed evitare circoli viziosi.
from collections import deque
def shortest_path(S, start, end):
"""
Trova il percorso di minima lunghezza tra start e end nell'insieme connesso S.
Restituisce la lista di celle del percorso e la lunghezza.
"""
if start not in S or end not in S:
return None, float('inf')
if start == end:
return [start], 0
# Coda per BFS: (cella, percorso fino a qui)
queue = deque([(start, [start])])
visited = set([start])
while queue:
current, path = queue.popleft()
# Esplora i vicini
x0, y0 = current
for x, y in [(x0+1, y0), (x0-1, y0), (x0, y0+1), (x0, y0-1)]:
if (x, y) in S and (x, y) not in visited:
new_path = path + [(x, y)]
if (x, y) == end:
return new_path, len(new_path) - 1 # Numero di passi
visited.add((x, y))
queue.append(((x, y), new_path))
return None, float('inf') # Nessun percorso trovato
S = {(0,0), (1,0), (2,0), (2,1), (1,1), (1,2), (0,2), (-1,2), (-1,1)}
path, l = shortest_path(S, (0,0), (-1,1))
plot_S(S,path)
{'lunghezza':l}
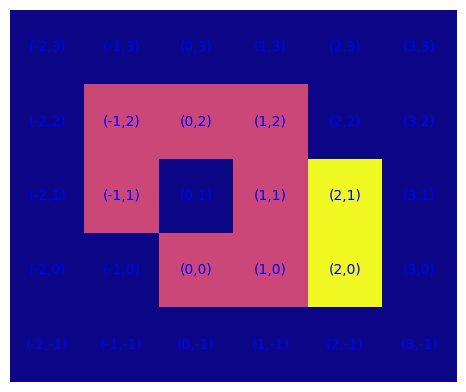
{'lunghezza': 6}
Ecco poi come trovare il percorso minimo tra due estremi del polimino.
S, _ = genera(100)
lstx, lsty = zip(*S)
x_min, x_max = min(lstx), max(lstx)
plot_S(S,
shortest_path(S,
(x_min,min(y for (x,y) in S if x==x_min)),
(x_max,max(y for (x,y) in S if x==x_max)))[0],
coord=False)
