L'esagono regolare è il terzo e ultimo poligono regolare che può tassellare il piano, rendendolo un altro candidato naturale per la generalizzazione dei polimini. Poiché l'esagono regolare è scomponibile in sei triangoli equilateri, ogni forma che otteniamo con questa base si può ottenere anche con triangoli equilateri come base, ovvero i poliesagoni sono un sottinsieme dei poliamanti.
L'interesse per i poliesagoni riguarda anche la loro connessione con strutture naturali (alveari) e chimiche (idrocarburi aromatici come il benzene, la cui struttura si basa su anelli esagonali).
def plot_Poliesagono(S):
fig, ax = plt.subplots()
ax.set_aspect('equal')
for (x, y) in S:
if y % 2 == 0:
x0 = x * np.sqrt(3)
y0 = y + y//2
vertices = [
(x0 + np.sqrt(3) / 2, y0 + 1/ 2),
(x0, y0 + 1),
(x0 - np.sqrt(3) / 2, y0 + 1/ 2),
(x0 - np.sqrt(3) / 2, y0 - 1/ 2),
(x0, y0 -1),
(x0 + np.sqrt(3) / 2, y0 - 1/ 2)]
else:
x0 = (x-1/2) * np.sqrt(3)
y0 = y + y//2 +1/2
vertices = [
(x0 + np.sqrt(3) / 2, y0 + 1/ 2),
(x0, y0 + 1),
(x0 - np.sqrt(3) / 2, y0 + 1/ 2),
(x0 - np.sqrt(3) / 2, y0 - 1/ 2),
(x0, y0 -1),
(x0 + np.sqrt(3) / 2, y0 - 1/ 2)]
triangle = patches.Polygon(vertices, closed=True, facecolor='lightblue',edgecolor='black', linewidth=1)
ax.add_patch(triangle)
ax.text(x0,y0, f"{x},{y}",horizontalalignment='center')
ax.axis('off')
ax.set_xlim((min(x for x,_ in S)-1)* np.sqrt(3), max(x for x,_ in S)* np.sqrt(3)+1)
ax.set_ylim(min(y+y//2 for _,y in S)-2, max(y+y//2 for _,y in S)+2)
# Impostazione tick interi per entrambi gli assi
ax.set_xticks(range(min(x for x,_ in S)-1, max(x for x,_y in S)+1))
ax.set_yticks(range(min(y for _,y in S)-1, max(y for _,y in S)+1))
#ax.grid(True)
plt.show()
plot_Poliesagono({(-1,0),(-1,-1),(0,-1), (0,0),(0,1),(1,1),(2,0),(0,2)})
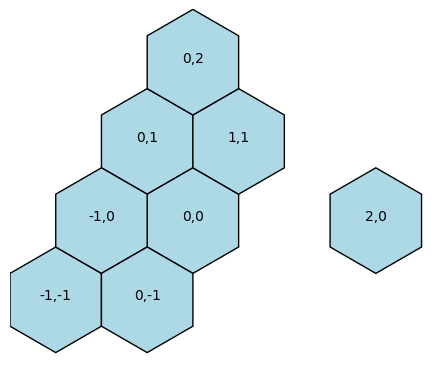
Per generare insiemi connessi di un dato numero di esagoni regolari, le forme dei poliesagoni, da un esagono iniziale in Python si può procedere nel modo seguente.
def generaPoliesagono(n):
S = {(0,0)}
B = {(1,0), (1,1), (0,1), (-1,0), (0,-1), (1,-1)}
for i in range(n-1):
(x,y) = random.choice(tuple(B))
S.add((x,y))
B.remove((x,y))
if y%2 == 0:
B = B | {(x+1,y), (x+1,y+1), (x,y+1), (x-1,y), (x,y-1), (x+1,y-1) } - S
else:
B = B | {(x+1,y), (x,y+1), (x-1,y+1), (x-1,y), (x-1,y-1), (x,y-1)} - S
return S, B
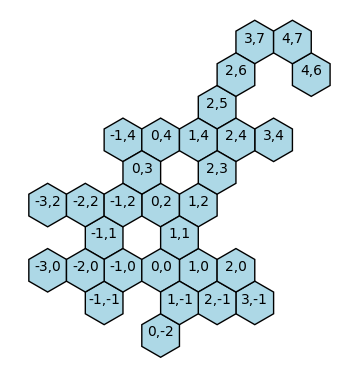
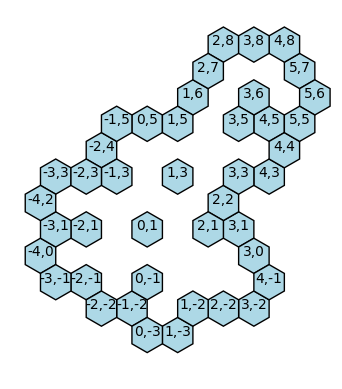
S, B = generaPoliesagono(30)
plot_Poliesagono(S), plot_Poliesagono(B)
- Polyhex, From Wikipedia, the free encyclopedia