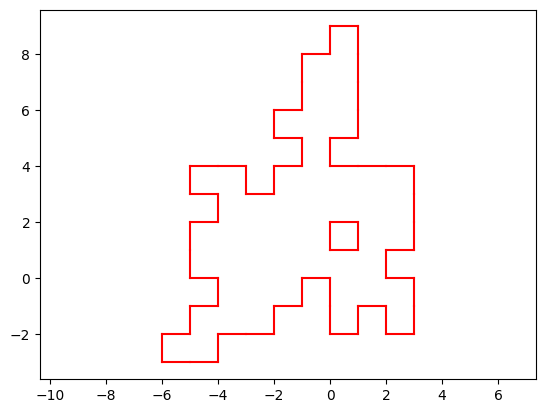
Linea perimetrale dei polimini
La linea perimetrale di un polimino, formata dai lati non condivisi, si può ottenere nel modo seguente.
def latiEsp(S):
if not S:
return None
le = []
for (x, y) in S:
if (x+1,y) not in S:
le += [((x+1,y),(x+1,y+1))]
if (x,y+1) not in S:
le += [((x,y+1),(x+1,y+1))]
if (x-1,y) not in S:
le += [((x,y),(x,y+1))]
if (x,y-1) not in S:
le += [((x,y),(x+1,y))]
return le
S, _ = genera(50)
for (x1, y1), (x2, y2) in latiEsp(S):
plt.plot([x1, x2], [y1, y2], 'r-')
plt.axis('equal')
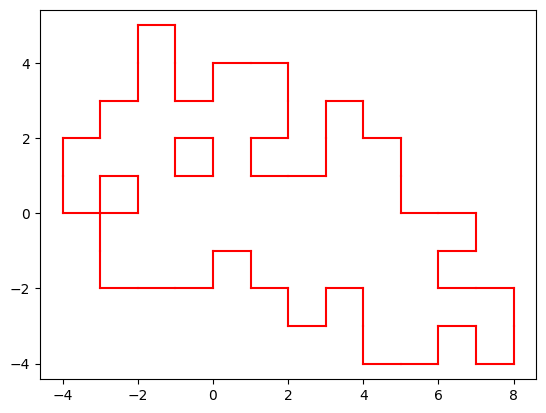
Si può anche considerare i lati di ciascun quadrato tutti orientati in verso antiorario. I lati interni saranno stati percorsi in un verso e anche in quello opposto.
def lineaPerim(S):
lati = set()
for (x, y) in S:
# Ogni cella ha 4 lati: rappresentiamoli come coppie di punti
lati_cella = {
((x, y), (x+1, y)), # lato basso
((x+1, y), (x+1, y+1)), # lato destro
((x+1, y+1), (x, y+1)), # lato alto
((x, y+1), (x, y)) # lato sinistro
}
for e in lati_cella:
# Se il lato è già presente al contrario, è interno → rimuovilo
if (e[1], e[0]) in lati:
lati.remove((e[1], e[0]))
else:
lati.add(e)
return lati
S, _ = genera(50)
for (x1, y1), (x2, y2) in lineaPerim(S):
plt.plot([x1, x2], [y1, y2], 'r-')
plt.axis('equal')
A parità dell'area, il numero $n$ di quadrati di cui si compone, il perimetro di un polimino è variabile. Se $L$ è il numero di lati condivisi, il perimetro è $4n-2L$.
def lati_comuni(S):
lati = set()
for (x, y) in S:
# Controlliamo solo "verso destra" e "verso l'alto"
# per evitare di contare due volte gli stessi lati
for v in {(x + 1, y), (x, y + 1)} & S:
lati.add(((x, y), v))
return lati
La lunghezza del perimetro di un polimino è anche pari al numero dei lati esposti
def perim(S):
if not S:
return None
p = 0
# Calcola il
for (x, y) in S:
p += len({(x+1,y), (x-1,y), (x,y+1), (x,y-1)} - S)
return p
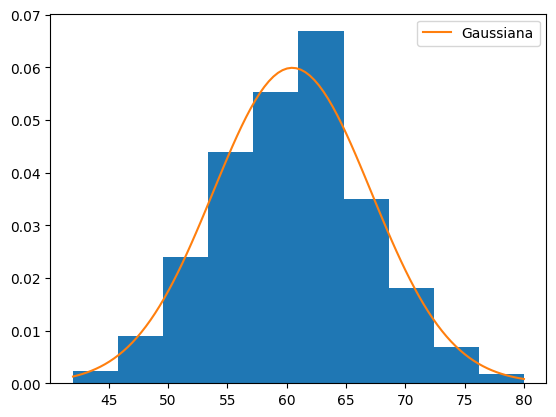
Può essere interessante osservare che la distribuzione dei perimetri sembra essere la normale.
n = 50
dati = []
for _ in range(1000):
S, _ = genera(n)
dati.append(perim(S))
plt.hist(dati,density=True)
media, sigma = np.mean(dati), np.std(dati)
x = np.linspace(min(dati), max(dati), 100)
plt.plot(x, 1/np.sqrt(2*np.pi*sigma**2)*np.exp(-(x-media)**2/(2*sigma**2)), label='Gaussiana')
plt.legend()