Consideriamo le trasfigurazioni di un polimino per effetto di un casuale slittamento di una sua cella dal bordo interno a quello esterno con conseguenti eventuali slittamenti di altre celle per conservare la connessione, cioè cambiamenti "minimi" del polimino dopo i quali la forma resta ancora quella di un polimino con lo stesso numero di elementi.
Ci si può chiedere se un tale cambiamento sia equivalente a quello prodotto più semplicemente dal "salto" di una cella del polimino che non spezza la connessione, quindi non un punto di articolazione, in una cella del suo bordo esterno, a contatto con un'altra cella del polimino.
Si potrebbe descrivere quest'altro tipo di movimento in modo concettualmente semplice scomponendolo in due fasi: nella prima si "espande" il polimino aggiungendo una nuova cella adiacente e poi nella seconda lo si "contrae" rimuovendo un'altra cella del polimino in modo da non spezzarne la connessione.
Altrimenti detto, prima si ha lo slittamento di una cella del polimino dal bordo interno a quello esterno, poi un'altra cella tra quelle che non ne pregiudicano la connessione salta a colmare il vuoto lasciato dalla prima.
def trasf(S):
B = bordoEst(S)
# seleziono una cella b dal bordo che sarà occupata da una cella di S
b = random.choice(tuple(B))
S.add(b)
# considero un insieme di celle non spostabili
nonSpostabili = {b}
# seleziono una cella s tra quelle spostabili che mantengono la connessione
s = random.choice(tuple(S - nonSpostabili))
while not is_polimino(S - {s}):
nonSpostabili.add(s)
s = random.choice(tuple(S -nonSpostabili))
S.remove(s)
return S
S, _ = genera(5)
for _ in range(3):
plot_S(S)
S = trasf(S)

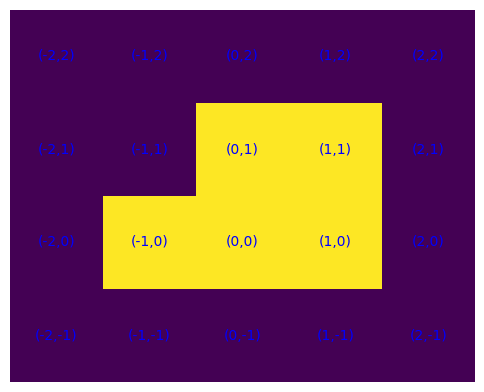
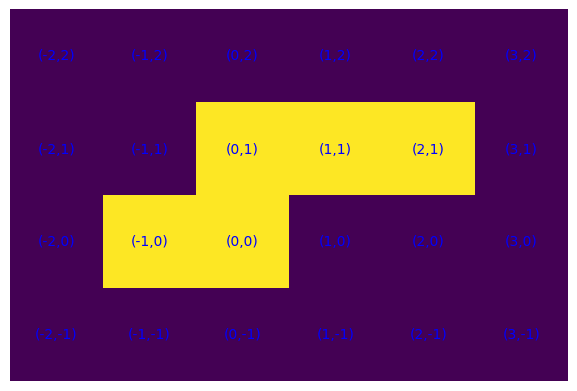
Senza consentire salti, che richiedono di uscire dalle due dimensioni, dopo aver fatto scivolare oltre il bordo una cella, fintantoché l'insieme non risulti connesso occorrerà spostare una cella di S adiacente al posto rimasto vuoto.
def trasf(So):
S = So
B = bordoEst(So)
# seleziono una cella b dal bordo che sarà poi occupata da una cella di S
b = random.choice(tuple(B))
S.add(b)
B.remove(b)
# tra gli elementi di S vicini a b seleziono la cella che, senza rompere la connessione,
# sarà quella passata in b lasciando una lacuna, elemento del bordo esterno
x, y = b
s = random.choice(tuple({(x+1,y), (x,y+1), (x-1,y),(x,y-1)} & S))
S.remove(s)
B.add(s)
while not is_polimino(set(S)):
# dovrò colmare la lacuna lasciata da s con un altro elemento di S vicino
x, y = s
Vs = {(x+1,y), (x,y+1), (x-1,y),(x,y-1)} & S - {b}
if Vs:
S.add(s)
s = random.choice(tuple(Vs))
S.remove(s)
B.add(s)
else:
return So
return S
S, _ = genera(5)
for _ in range(3):
plot_S(S)
S = trasf(S)
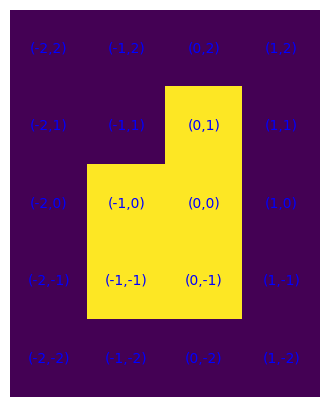
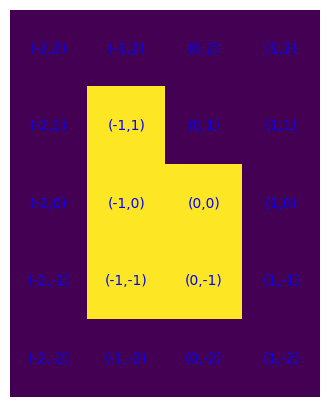
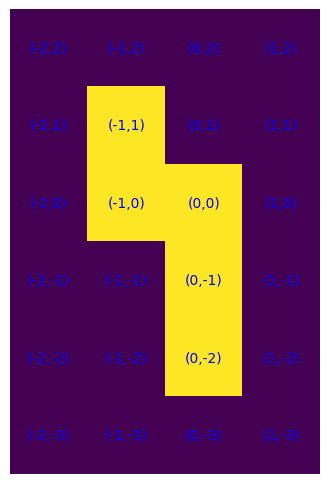
Del resto, poiché la condizione di connessione significa che due celle qualsiasi di S possono essere unite da un cammino composto da passi unitari verticali e orizzontali in modo tale che ogni cella del cammino giaccia in S, allora da una cella qualunque a una cella di frontiera si possono fare scorrere tutte le celle del cammino che le connette lungo il cammino stesso. Con ciò risulta che le due modalità sono equivalenti.
Si può osservare che il movimento precedentemente descritto tende ad "assottigliare" il polimino, che il cambiamento avviene probabilmente più che altro a spese delle celle interne.
Si potrebbe allora, per colmare la lacuna lasciata da uno slittamento verso il bordo esterno, scegliere unicamente del bordo interno, purché non precluda la connessione, la cella che farà da tappabuco.
def trasf(S):
B = bordoEst(S)
# seleziono quale cella del bordo espandersi a spese di una del bordo interno
b = random.choice(tuple(B))
S.add(b)
# seleziono dal bordo interno di S che non compromettono la connessione
Bi= set()
for (x,y) in B:
if (x+1,y) in S and is_polimino(S - {(x+1,y)}): Bi.add((x+1,y))
if (x-1,y) in S and is_polimino(S - {(x-1,y)}): Bi.add((x-1,y))
if (x,y+1) in S and is_polimino(S - {(x,y+1)}): Bi.add((x,y+1))
if (x,y-1) in S and is_polimino(S - {(x,y-1)}): Bi.add((x,y-1))
S.remove(random.choice(tuple(Bi)))
return S
Possiamo modificare l'algoritmo anche più restrittivamente considerando solo le celle intorno a quella slittata, se non spezzano la connessione, per fare da tappabuchi.
def trasf(S):
B = bordoEst(S)
# seleziono quale cella del bordo espandersi
x, y = random.choice(tuple(B))
# seleziono i vicini di S che non compromettono la connessione
Vxy = set()
for s in {(x+1,y), (x,y+1), (x-1,y),(x,y-1)} & S:
if is_polimino((S | {(x,y)}) - {s}):
Vxy.add(s)
while not Vxy:
B.remove((x,y))
x, y = random.choice(tuple(B))
Vxy.clear()
for s in {(x+1,y), (x,y+1), (x-1,y),(x,y-1)} & S:
if is_polimino((S | {(x,y)}) - {s}):
Vxy.add(s)
if Vxy:
S.add((x,y))
S.remove(random.choice(tuple(Vxy)))
return S
In questo modo il polimino assume l'aspetto di un organismo che muta la sua forma mantenendo inalterata la massa.