Possiamo generare in modo casuale polimini di un dato numero di elementi.
Ad esempio possiamo costruire incrementalmente l'insieme di celle iniziando da un quadrato, includere a caso un elemento del suo bordo (o frontiera o limite o confine) esterno, aggiornare il bordo esterno di questo nuovo insieme di celle, includere nuovamente a caso un elemento del bordo esterno e così via.
import random
def genera(n):
S = {(0,0)}
B = {(1,0), (0,1), (-1,0),(0,-1)}
for i in range(n-1):
(x,y) = random.choice(tuple(B))
S.add((x,y))
B.remove((x,y))
B = B | {(x+1,y), (x,y+1), (x-1,y), (x,y-1)} - S
return S, B
genera(4)
({(-1, -1), (0, -1), (0, 0), (0, 1)},
{(-2, -1),
(-1, -2),
(-1, 0),
(-1, 1),
(0, -2),
(0, 2),
(1, -1),
(1, 0),
(1, 1)})
S, B = genera(4)
plot_S(S), plot_S(B)
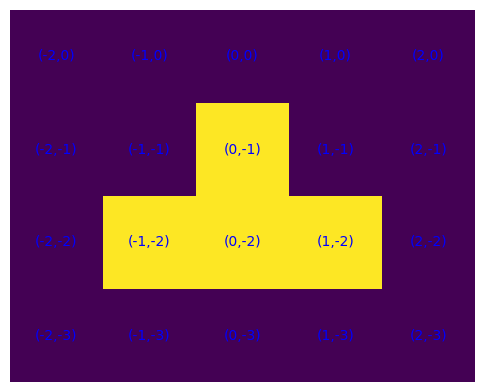
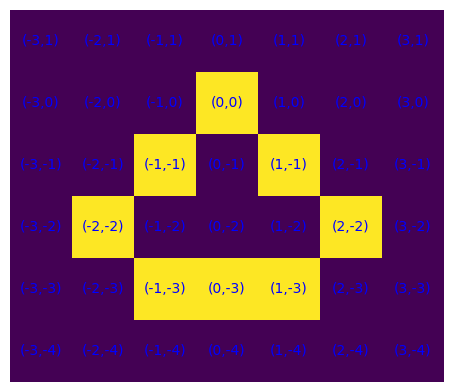
is_polimino(S), is_polimino(B)
(True, False)
Volendo invece basarsi su quel che si può chiamare bordo (o frontiera o limite o confine) interno e incrementare il polimino aggiungendo volta per volta un quadrato a caso adiacente a un quadrato scelto a caso del bordo interno, il procedimento si complica un po'. Infatti quell'elemento aggiunto potrebbe diventare interno al polimino o rinchiudere all'interno qualche suo vicino del bordo interno.
def genera(n):
S = {(0,0)}
F = {(0,0)}
for i in range(n-1):
x, y = random.choice(tuple(F))
x, y = random.choice(tuple({(x+1,y), (x,y+1), (x-1,y), (x,y-1)} - S))
S.add((x,y))
if len({(x+1,y), (x,y+1), (x-1,y), (x,y-1)} & S)<4:
F.add((x,y))
for x, y in ({(x+1,y), (x,y+1), (x-1,y), (x,y-1)} & F):
if len({(x+1,y), (x,y+1), (x-1,y), (x,y-1)} & S)==4:
F.remove((x,y))
return S, F
S, F = genera(20)
plot_S(S), plot_S(F)


is_polimino(S), is_polimino(F)
(True, False)
L'algoritmo è simile al modello proposto da Murray Eden in A Two-dimensional Growth Process nel 1961, per simulare la crescita di tessuti biologici, in particolare tumori. La crescita avviene in modo stocastico: a ogni passo, una cellula tumorale può proliferare in una delle celle adiacenti vuote. Basato su regole semplici, il modello di Eden è capace di generare strutture complesse simili a quelle osservate nei processi di proliferazione cellulare. La crescita è localizzata: solo le cellule sul bordo del tumore possono generare nuove cellule. Non si tiene conto della morte cellulare o della migrazione: è un modello di pura crescita.
Un altro algoritmo di generazione casuale, una crescita stocastica con backtracking tipo DFS, genera labirinti "sfilati" che ricordano percorsi labirintici.
def genera_polimino_labirintico(n):
S = {(0, 0)}
stack = [(0, 0)]
while len(S) < n and stack:
x, y = stack[-1]
# Trova vicini liberi
vicini_liberi = []
for x, y in {(x+1,y), (x-1,y), (x,y+1), (x,y-1)}-S:
# Controlla che non tocchi troppo altre celle (labirintico)
if len( {(x+1,y), (x-1,y), (x,y+1), (x,y-1)} & S) <= 1:
vicini_liberi.append((x, y))
if vicini_liberi:
# Scegli uno dei vicini possibili
s = random.choice(vicini_liberi)
S.add(s)
stack.append(s)
else:
# Backtrack se bloccato
stack.pop()
return S
plot_S(genera_polimino_labirintico(500))

Per generare labirinti dai quali ottenere polimini davvero labirintici possiamo partire da un algoritmo per generare labirinti come il seguente.
def make_maze(w = 16, h = 8):
vis = [[0] * w + [1] for _ in range(h)] + [[1] * (w + 1)]
ver = [["| "] * w + ['|'] for _ in range(h)] + [[]]
hor = [["+-"] * w + ['+'] for _ in range(h + 1)]
def walk(x, y):
vis[y][x] = 1
d = [(x - 1, y), (x, y + 1), (x + 1, y), (x, y - 1)]
shuffle(d)
for (xx, yy) in d:
if vis[yy][xx]: continue
if xx == x: hor[max(y, yy)][x] = "+ "
if yy == y: ver[y][max(x, xx)] = " "
walk(xx, yy)
walk(randrange(w), randrange(h))
maze = ""
for (a, b) in zip(hor, ver):
maze += ''.join(a + ['\n'] + b + ['\n'])
return maze
maze = make_maze()
print(maze)
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
| | | |
+-+-+ +-+ + +-+-+-+-+ + +-+ + +-+
| | | | | | | | |
+ +-+-+ +-+-+-+ + + + +-+ + +-+ +
| | | | | | | | | | |
+-+ + + +-+-+-+-+-+-+ + + +-+ + +
| | | | | | | |
+-+-+ +-+ +-+-+ + +-+-+ +-+ +-+ +
| | | | | | | | | |
+ + +-+ +-+ + + + +-+ +-+-+-+-+ +
| | | | | | | | |
+ +-+-+-+ + + + +-+ +-+-+-+ + + +
| | | | | | | | | |
+-+ + +-+-+ + +-+ + + +-+ +-+-+ +
| | | | | |
+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+
Da qui possiamo ottenere il polimino che rappresenta le pareti del labirinto.
def inGriglia(maze):
m = maze.split('\n')
S = set()
for y in range(len(m)-2):
for x in range(len(m[0])):
if m[y][x] != " ":
S.add((x,y))
return S
plot_S(inGriglia(maze))

Alternativamente possiamo ottenere il polimino che rappresenta i percorsi.
def inGrigliaP(maze):
m = maze.split('\n')
S = set()
for y in range(len(m)-2):
for x in range(len(m[0])):
if m[y][x] == " ":
S.add((x,y))
return S
plot_S(inGrigliaP(maze))

Un altro algoritmo di generazione casuale di polimini prevede, anziché espanderlo a partire da un centro, di crearlo a partire da una certa distanza dal centro con un cammino casuale che converga verso il polimino che si va così creando, le cui punte crescono più velocemente perché sono più facili da "toccare". Si tratta di un procedimento del tipo Diffusion-Limited Aggregation (DLA), processo stocastico che genera strutture ramificate attraverso l'aggregazione di particelle che si muovono casualmente.
def generaDLA(n):
S = {(0,0)}
while len(S) < n:
angle = random.uniform(0, 2 * np.pi)
x = int(2 * n * np.cos(angle))
y = int(2 * n * np.sin(angle))
walk = []
for _ in range(1000*n):
while (x,y) not in S:
walk.append((x,y))
x, y = random.choice([(x+1,y),(x,y+1),(x-1,y),(x,y-1)])
if abs(x) + abs(y) > 2*n:
walk = []
break
S = S.union(set(walk))
return S
plot_S(generaDLA(100))
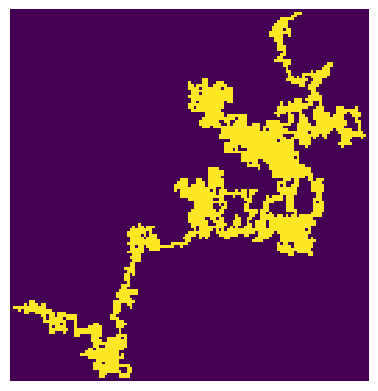
Oltre a cambiare alcuni parametri come la distanza dal centro da cui partono le particelle, si possono considerare varianti per simulare attrazione verso il polimino che via via si crea, o per seguire direzioni predefinite da un campo.
- Diffusion-limited aggregation, From Wikipedia, the free encyclopedia