Polimini

Dimensioni frattali dei polimini

La dimensione frattale, concetto reso popolare da Benoît Mandelbrot negli anni '70, fornisce uno strumento potente per quantificare la complessità di oggetti geometrici. Tradizionalmente applicata a forme continue, la dimensione frattale può essere adattata per studiare strutture discrete come i polimini, rivelando caratteristiche nascoste della loro morfologia e fornendo una misura della complessità geometrica di queste strutture. La dimensione frattale $D$ può essere pensata come la potenza del fattore di scala $\frac{1}{\epsilon}$ della misura $N$ di un oggetto data una certa scala del suo "raggio".

Se $\mathcal{F}$ è una figura piana e $N(\varepsilon)$ il numero minimo di quadrati di lato $\varepsilon$ necessari per ricoprire $P$, la dimensione box-counting è definita come: \[ \dim_B(\mathcal{F}) = \lim_{\varepsilon \to 0} \log_\frac{1}{\varepsilon} N(\varepsilon) = \lim_{\varepsilon \to 0} \frac{\log N(\varepsilon)}{\log\frac{1}{\varepsilon}} \] Le proprietà frattali emergono naturalmente anche in strutture discrete. Per una figura piana come un cerchio, un quadrato, un polimino, occorrerà distinguere tra dimensione frattale della figura e dimensione frattale della linea che ne costituisce il bordo.
I polimini possono essere classificati in tre categorie principali basate sulla loro dimensione frattale:

Polimini compatti ($\dim_B \approx 2$): Forme che tendono a riempire efficientemente lo spazio.
Polimini ramificati ($1 < \dim_B < 2$): Forme con struttura dendritica che esibiscono proprietà frattali intermedie.
Polimini lineari ($\dim_B \approx 1$): Forme essenzialmente unidimensionali.

Uno degli indicatori più significativi del carattere frattale di un polimino è la relazione tra il suo perimetro $P$ e la sua area $A$. Per forme euclidee regolari, vale tipicamente $P \propto A^{1/2}$, mentre per frattali puri si ha $P \propto A^{D/2}$ dove $D\gt 1$ è la dimensione frattale del bordo, in particolare $D\approx 2$ per strutture filamentose.

Per una famiglia di polimini $\{P_n\}$ con $n \to \infty$, indicato con $P(n)$ il perimetro, ed essendo l'area $A(n) = n$, se esiste un esponente $D$ tale che: \[ P(n) \propto n^\frac{D}{2} \] allora $D$ è la dimensione frattale del bordo del polimino.

def stima_dim_fratt(Ss):
    logn, logP = [], []
    for S in Ss:
        logP.append(np.log(perim(S)))
        logn.append(np.log(len(S)))
    slope = np.polyfit(logn, logP, 1)[0]
    Df = 2*slope
    plt.plot(logn, logP, 'o-')
    plt.xlabel("log n")
    plt.ylabel("log P")
    plt.title(f"Stima dimensione frattale Df ≈ {Df:.2f}")
    plt.show()

stima_dim_fratt( [genera(n)[0] for n in [10,20,40,80,160,320]])

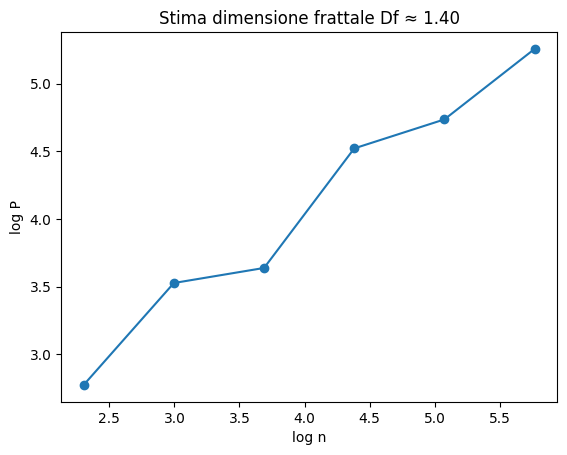
stima_dimensione_frattale( [genera_polimino_labirintico(n) for n in [10,20,40,80,160,320]])

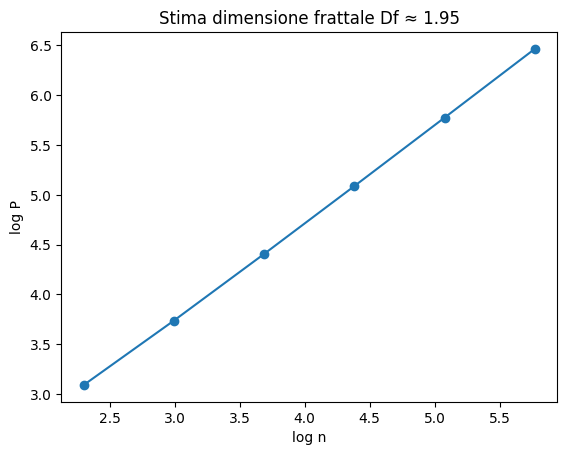
stima_dimensione_frattale( [genera_DLA(n) for n in [10,20,40,80,160,320]])

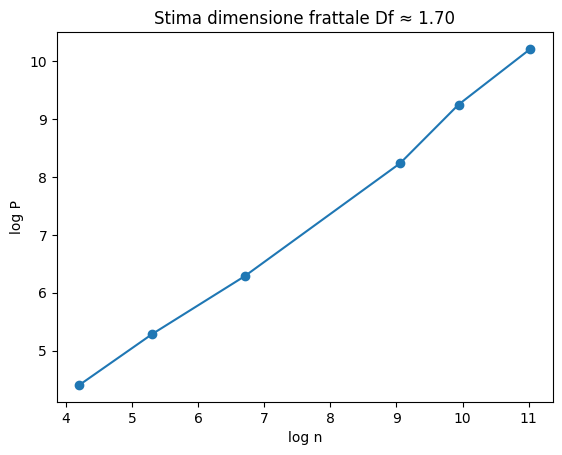
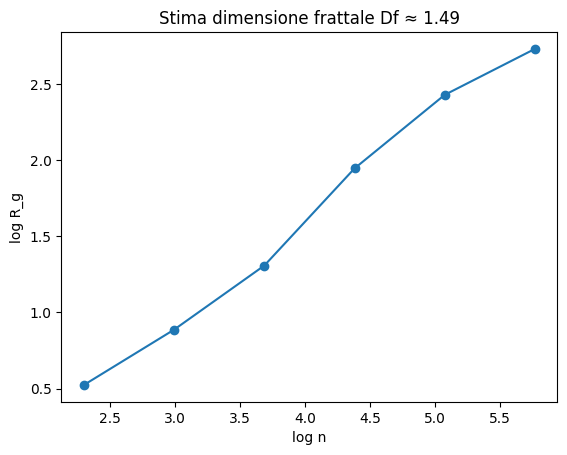
Per polimini frattali possiamo usare anche il raggio di girazione, che fornisce la densità e compattezza del corpo, per la dimensione frattale del polimino.

Se esiste una legge di scala: \[ R_g \propto n^\frac{1}{D} \] allora $D$ è la dimensione frattale (in senso statistico) del polimino.

def stima_dimensione_frattale(Ss):
    logn, logR = [], []
    for S in Ss:
        logR.append(np.log(raggio_girazione(S)))
        logn.append(np.log(len(S)))
    slope = np.polyfit(logn, logR, 1)[0]
    Df = 1/slope
    plt.plot(logn, logR, 'o-')
    plt.xlabel("log n")
    plt.ylabel("log R_g")
    plt.title(f"Stima dimensione frattale Df ≈ {Df:.2f}")
    plt.show()

stima_dimensione_frattale( [genera(n)[0] for n in [10,20,40,80,160,320]])

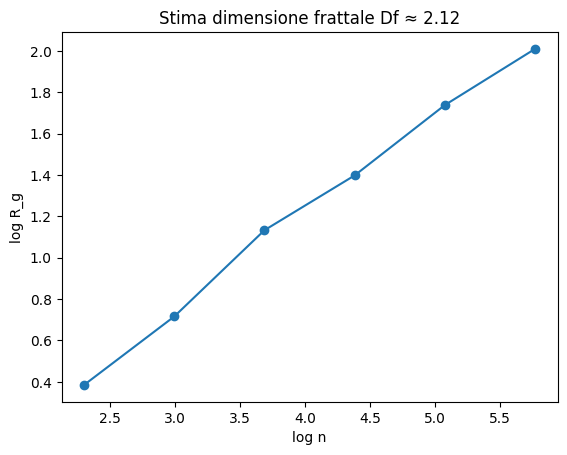
stima_dimensione_frattale( [genera_polimino_labirintico(n) for n in [10,20,40,80,160,320]])

stima_dimensione_frattale( [genera_DLA(n) for n in [10,20,40,80,160,320]])

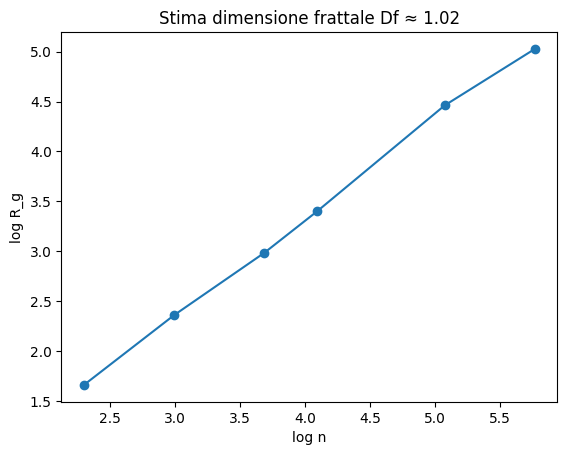
Esiste dunque una chiara relazione tra la morfologia dei polimini e i processi che li generano. Modelli di crescita come il modello di Eden o il Diffusion-Limited Aggregation producono polimini con dimensioni frattali caratteristiche

Per approfondimenti:

Fractal dimension, From Wikipedia, the free encyclopedia