Sono figure piane create unendo più triangoli retti isosceli identici, cateto con cateto o ipetenusa con ipotenusa. La connessione con i polimini è molto stretta poiché il triangolo base è "mezzo quadrato" e quindi molti poliaboli corrispondono a polimini.
Sono anche questi una generalizzazione dei polimini ma con una complessità aggiuntiva: a differenza di quadrati, triangoli equilateri ed esagoni regolari non sono poligoni regolari. La regola che "lati uguali si uniscono a lati uguali" crea vincoli unici e rende i problemi di tassellazione diversi e spesso più difficili.
| Numero di Triangoli | Nome | Numero di Forme "Libere" |
| 1 | Monabolo | 1 |
| 2 | Diabolo | 3 |
| 3 | Triabolo | 4 |
| 4 | Tetrabolo | 14 |
| 5 | Pentabolo | 30 |
| 6 | Esabolo | 107 |
| 7 | Eptabolo | 318 |
| 8 | Octabolo | 1117 |
import math
def plot_Poliabolo(S):
fig, ax = plt.subplots(figsize=(8, 8))
min_x, max_x, min_y, max_y = math.inf, -math.inf, math.inf, -math.inf
for (x, y, t) in S:
# Ottieni i vertici relativi del triangolo
vertici = {
0: [(x, y), (x+1, y), (x, y+1)],
1: [(x, y), (x+1,y), (x+1, y+1)],
2: [(x+1, y), (x+1, y+1), (x, y+1)],
3: [(x,y), (x+1, y+1), (x, y+1)],
}
# Crea il poligono e aggiungilo al grafico
polygon = Polygon(vertici[t], edgecolor='black', facecolor='skyblue', linewidth=1.5)
ax.add_patch(polygon)
# Aggiorna i limiti per centrare il grafico
for vx, vy in vertici[t]:
min_x, max_x = min(min_x, vx), max(max_x, vx)
min_y, max_y = min(min_y, vy), max(max_y, vy)
# Impostazioni del grafico
ax.set_aspect('equal', adjustable='box')
ax.set_xlim(min_x -1, max_x + 1)
ax.set_ylim(min_y - 1, max_y + 1)
ax.set_title(f'Insieme di {len(S)} Elementi')
plt.axis('off')
plt.show()
plot_Poliabolo({(0,0,1),(0,0,3),(0,1,2),(1,0,0)})
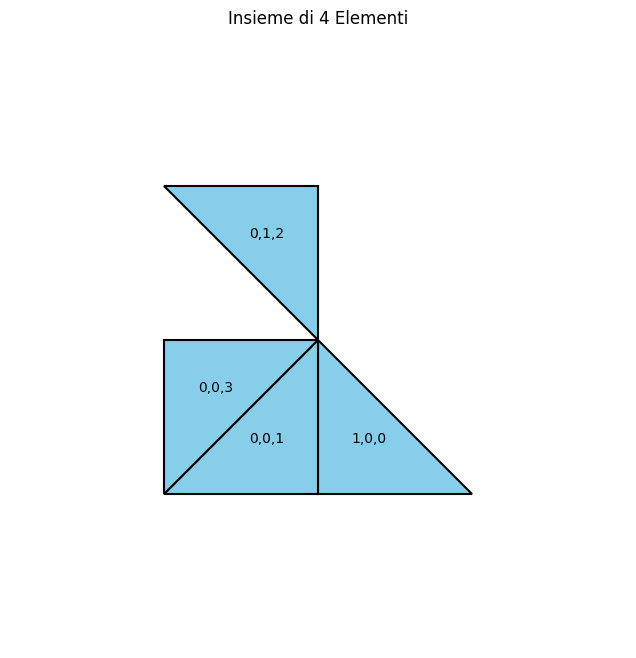
Per generare insiemi connessi di un dato numero di triangoli rettangoli isosceli, le forme dei poliaboli, da un triangolo iniziale in Python si può procedere nel modo seguente.
def genera_Poliabolo(n):
# Inizia con un singolo triangolo casuale al centro
t = random.randint(0, 3)
S = {(0, 0, t)}
vicinato = {
# Vicini del triangolo (0,0,0)
0: [(0, 0, 2),(-1, 0, 1),(-1, 0, 1),(0, -1, 2),(0,-1,3)],
# Vicini del triangolo (0,0,1)
1: [(0, 0, 3),(1, 0, 0),(1,0,3),(0, -1, 2),(0,-1,3)],
# Vicini del triangolo (0,0,2)
2: [(0, 0, 0),(1, 0,0),(1,0,3),(0, 1, 0),(0,1,1)],
# Vicini del triangolo (0,0,3)
3: [(0, 0, 1), (-1, 0, 1),(-1,0,2),(0,1,0),(0,1,1) ]
}
# Nel bordo esterno possono essere aggiunti triangoli
B = set(vicinato[t])
while len(S) < n:
# Scegli un candidato casuale dal bordo
x, y, t = random.choice(list(B))
S.add((x, y, t))
B.remove((x, y, t))
if (x, y, (t+1)%2) in B: B.remove((x, y, (t+1)%2))
if (x, y, (t+1)%2+2) in B: B.remove((x, y, (t+1)%2+2))
# Aggiorna il bordo con i vicini del nuovo triangolo
for dx, dy, tv in vicinato[t]:
xv, yv = x + dx, y + dy
# Aggiungi il vicino solo se non fa già parte di S o non si sovrappone parzialmente
if (xv,yv,tv) not in S and (xv,yv, (tv+1)%2) not in S and (xv,yv, (tv+1)%2+2) not in S:
B.add((xv,yv,tv))
return S, B
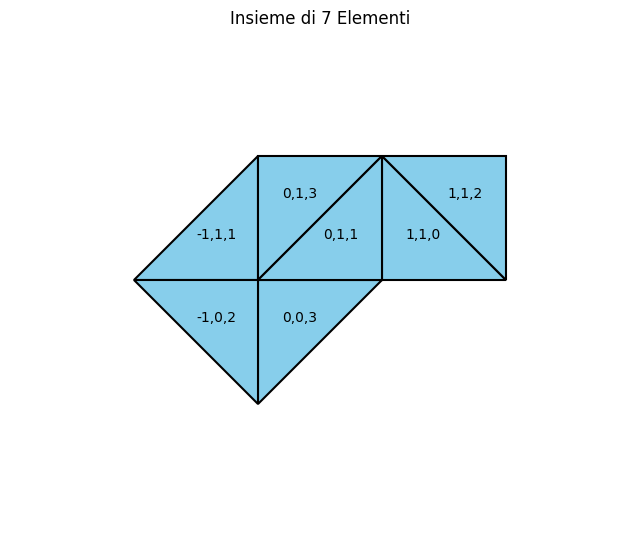
S, _ = genera_Poliabolo(7)
plot_Poliabolo(S)
- Polyabolo, From Wikipedia, the free encyclopedia