Quadrati magici
Lo Yod primitivo è appoggiato su nove pilastri che lo sostengono.
Questi nove pilastri sono disposti nelle nove direzioni del mondo.
Sono disposti in linee rette, tre in ogni direzione ed uno al centro.
Questi tre punti disposti in quadrato fanno nove, che in realtà non sono che otto.
Sono i troni del sacro Yod.
Libro dello Zohar II/180
On magic squares
di Leonard EulerDelivered to the St. Petersburg Academy October 17, 1776. Originally published as De quadratis magicis, Commentationes arithmeticae
Magic Squares
su wikipedia
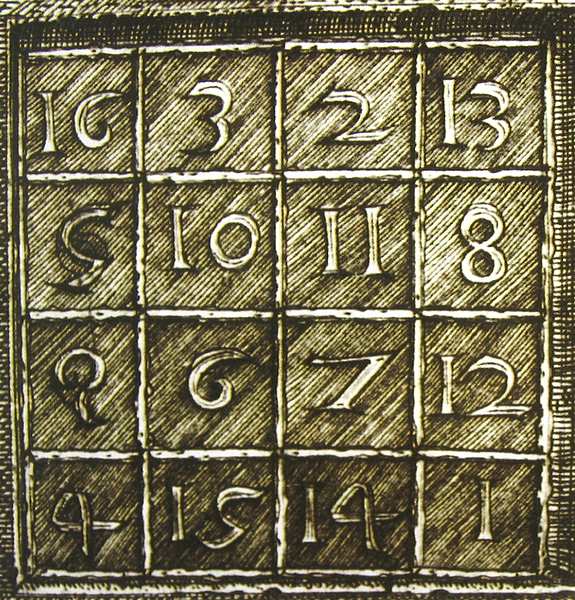
Melancholia di Dürer (1514) include il quadrato magico di ordine 4 con somma 34 ritagliato sotto il titolo di questa pagina.
Magic Squares
di Holger DanielssonMagic squares are rather old. According to legend the first known magic square was discovered by Emporor Yu in China about 2200 B.C. When he was walking on the banks of the Loh river, he saw a mystical turtle with some dots within squares on its shell.
The very first textual reference can be found, however, in the writings of Zhuang Zi (369-286 B.C.). In this representation, the odd numbers are represented by white dots (Yang symbols) and represent the sky, while the even numbers are shown as black dots (the Yin symbols), the symbol of the Earth.
La grande avventura matematica dei quadrati e dei cubi magici
di Federico PeirettiQuadrati e cubi magici sono straordinarie configurazioni numeriche, di grande tradizione. Ai confini tra il gioco e la matematica, sono un’affascinante sfida alla nostra intelligenza.
Leonhard Euler's Magic Square v1.0
di Oliver MerkelObjective is to drag bi-colored tiles forming a squared pattern on given board positions to match certain requirements as listed below. The size of the squared board is measured by its width in tiles. So if it is eight tiles wide and high the squared board has 64 positions. The amount of available different colors in the color palette matches the size of the board. Each of the rectangular shaped unique tiles has two combined attributes: a frame color and an inner color.
MAGIC SQUARES
di Carlos Alberto Roldão Lopes- Introductory Note
- Brief Early History
- Magic Squares: Basic Definitions
- Magic Squares: General Classification
- Magic Squares: Issue
Knight's Tour Notes
di George JellissThe following notes describe, to the best of my current knowledge, the main results (and a few sideshows) that have been achieved in the study of knight's tours and related questions.