Passeggiata in una direzione

Per primo analizziamo il caso in cui il moto avviene in una sola direzione: un ubriaco si muove lungo un percorso già segnato, per semplicità rettilineo, in un verso oppure in quello opposto, con uguale probabilità e passo costante.

Sia ad esempio n= il numero totale dei passi da compiuti.

Ogni volta, dopo ogni passo, la scelta di andare nel verso che considereremo positivo, +1, oppure nel verso opposto, – 1, è casuale, come lanciando ogni volta una moneta e seguire un verso o l'altro a seconda che esca testa oppure croce.

Possiamo simulare e studiare tali moti il computer servendosi della funzione random che ogni linguaggio di programmazione mette a disposizione per fornire numeri casuali, tutti con la stessa probabilità di essere scelti.

Con Javascript una scelta casuale tra due valori può essere fatta ad esempio elevando -1 a esponente 0 o 1 a caso

	Math.pow(-1,Math.round(Math.random()))

oppure come $2\delta -1$ con $\delta \in \{0,1\}$

	2*Math.floor(Math.random()*2) -1

oppure

	2*Math.round(Math.random()) -1

o anche, servendosi dell'operatore per alternative:

	(Math.random()<0.5)? -1: 1

Per creare una elenco o lista di queste scelte si ricorrerà a una iterazione:

	var v=[];
	for (var i=0; i<n; i++) v.push((Math.random()<0.5)? -1: 1);

oppure in una sola riga sfruttando i metodi per gli array:

	var v=new Array(n).fill().map(x => (Math.random()<0.5)? -1: 1);

ottenendo

Le posizioni occupate successivamente per effetto di queste scelte , \[\displaystyle pos(n+1)=pos(n)+passo(n)=pos(0)+\sum_{k=0}^npasso(k),\] possono così essere calcolate come somme cumulate:

	var pos=[];
	var sum=v[0];
	for (var i=1; i<n; i++){
		pos.push(sum);
		sum+=v[i]
	}

oppure in una sola riga:

	var pos=v.reduce((lst, x, i) => [...lst, x + (lst[i-1] || 0)], []);

o anche

	var pos=v.map((sum => value => sum += value)(0))

ottenendo

il cui grafico

Iniziamo col condurre alcune semplici riflessioni.

Le posizioni raggiunte dopo $n$ passi costituiscono una variabile aleatoria $X_n$:

N° di passi	valori di $X_n$: posizioni raggiunte
1	–1, +1
2	–2, 0 , +2
3	–3, –1, +1, +3
….
2n	–n,–n+1, … –4, –2, 0, +2, +4, …, n–1, n
2n+1	–n,–n+1 … –3, –1, +1, +3, …, n–1, n

Ciascuna di queste posizioni può essere raggiunta seguendo percorsi diversi:

N° di passi	N° di percorsi che conducono a ogni valore di $X_n$
1	1 , 1
2	1, 2 , 1
3	1, 3, 3, 1
….
n	$1, C_{n,1}, C_{n,2}, C_{n,3}, ..., C_{n,n-3}, C_{n,n-2}, C_{n,n-1}, 1 $

dove $C_{n,k}=C_{n-1,k-1}+C_{n-1,k}$ sono anche i coefficienti dello sviluppo del binomio $(1+x)^n$ ovvero le combinazioni di $n$ elementi presi $k$ alla volta e che formano uno schema numerico molto noto, il triangolo di Pascal-Tartaglia.

Il numero totale di percorsi effettuabili con n passi, la somma dei componenti la riga n-esima del triangolo di Pascal-Tartaglia, è 2ⁿ.

Nel modo più naturale, cioè ricorsivamente, questo schema, si può descrivere in javascript nel modo seguente:

function nPercorsi(n,x) {
	if (n==0) return 1
	else if(n<Math.abs(x) ) return 0
	else if((n+Math.abs(x))%2>0) return 0
	else if(n==Math.abs(x) ) return 1
	else return nPercorsi(n-1,x-1)+nPercorsi(n-1,x+1)
}

Si può ottenere anche iterando:

lst=[...lst,0].map((x, i) => x + [0,...lst][i])

che data la lista lst, inizialmente formata dal solo 1, corrispondente a una riga dello schema, forma la lista corrispondente alla riga successiva sommando la lista [0,...lst], nella quale si antepone a lst l'elemento 0, con la lista [...lst,0], nella quale lst viene prolungata con uno zero finale.

Quindi

var lst=[1]
for (var k=0; k<n; k++)
  lst=[...lst,0].map((x, i) => x + [0,...lst][i])

crea le prime n+1 righe.

n=4

1
1,1
1,2,1
1,3,3,1
1,4,6,4,1

Volendo inserire nello schema anche il numero, nullo, di percorsi per raggiungere posizioni pari per un numero dispari di passi o viceversa:

var lst=[1]; 
for(var i=0; i<n;i++){
  lst=[...lst,0,0].map((x,k)=>x+[0,0,...lst][k]);
}

n=4

1
1,0,1
1,0,2,0,1
1,0,3,0,3,0,1
1,0,4,0,6,0,4,0,1

Lo schema del triangolo numerico di Pascal-Tartaglia si può ottenere anche per diagonali iterando:

diag.map((sum => value => sum += value)(0)) 

che produce somme cumulate a partire dalla diagonale formata di tutti 1.

diag=new Array(n+1).fill(1) 

n=4

1	1	1	1	1
1	2	3	4
1	3	5
1	4
1

Il termine generico $C_{n,k}$, che si scrive anche $\binom{n}{k}$, si può ottenere calcolando $\frac{n!}{k!(n-k)!}=\frac{n(n-1)\cdots(n-k+1)}{k(k-1)\cdots 1}$ e quindi con Javascript anche nel modo seguente, arrotondando eventualmente il risultato:

 	var C=1;
	for (var i=1; i⁢=k; i++) C*=(n-k+i)/k;

oppure in una sola riga:

	new Array(k).fill().reduce((num,e,i)=>num*=(n-k+1+i)/(i+1),1)

Così ad esempio C()=10

Si può osservare che nello sviluppo di \[\displaystyle(x^{-1}+x)^n=\sum_{k=0}^n\binom{n}{k}x^{-n+k}x^{k}= \sum_{k=0}^n\binom{n}{k}x^{2k-n}\] gli esponenti di $x$ sono le posizioni raggiunte dopo gli $n$ passi e i coefficienti esprimono il numero di passeggiate diverse che conducono alla stessa posizione.

Indicando con $x=2k-n,\quad \mbox{con}\;\; k=0,1,2,...,n$ la posizione raggiunta se $n$ è il numero di passi, allora il numero di percorsi possibili per raggiungerla è $\binom{n}{\frac{n+x}{2}}=\binom{n}{\frac{n-x}{2}}$; si osservi che se indichiamo con $n_+$ il numero dei passi nel verso positivo e $n_-$ quello dei passi nel verso opposto, allora $\begin{cases}n_++n_-=n\\ n_+-n_-=x \end{cases}$ da cui $\begin{cases}n_+=\frac{n+x}{2}\\ n_-=\frac{n-x}{2} \end{cases}$.

Dunque la posizione raggiunta dopo $n$ passi è una variabile casuale $X_n$ che assume i valori \[-n, -n+1, \cdots, -1, 0, 1, \cdots, n-1, n\] e la cui distribuzione di probabilità, cioè la probabilità di raggiungere la posizione $x$ dopo $n$ passi, si può ottenere dividendo il numero di modi di raggiungere quella posizion per il numero totale $2^n$ di percorsi effettuabili. \[p(X_n=x)=\begin{cases}\binom{n}{\frac{n+x}{2}}\frac{1}{2^n} &\quad\mbox{se n+x è pari}\\ 0 &\quad\mbox{altrimenti}\end{cases}\]

Si può ottenere la distribuzione delle probabilità con una minima variazione del procedimento per determinare le righe del triangolo di Pascal-Tartaglia.

var lst=[1]
for (var k=0; k<n; k++)
  lst=[...lst,0].map((x, i) => (x + [0,...lst][i])/2)

n=4

1
0.5,0.5
0.25,0.5,0.25
0.125,0.375,0.375,0.125
0.0625,0.25,0.375,0.25,0.0625

o anche

n=4

1
0.5,0,0.5
0.25,0,0.5,0,0.25
0.125,0,0.375,0,0.375,0,0.125
0.0625,0,0.25,0,0.375,0,0.25,0,0.0625

È più chiaro, poiché sintetico, rappresentare graficamente la legge di dstribuzione, o come punti sul piano cartesiano o mediante istogramma.

n=4

Si tratta della distribuzione teorica.

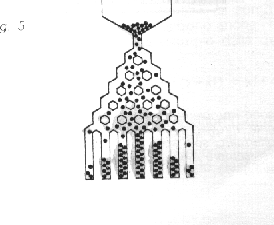
Nel dispositivo in figura, proposto a fine ‘800 da Francis Galton, delle palline vengono fatte scendere entro una griglia in cui dei chiodi costituiscono un ostacolo che la singola pallina può aggirare indifferentemente a destra o a sinistra. Ne deriva in modo meccanico un istogramma de descrive la distribuzione delle frequenze delle posizioni raggiunte.