Passeggiate casuali

La configurazione così ottenuta è il semitriangolo di Pascal. ( Catwalks, Sandsteps and Pascal Pyramids, Richard K. Guy). Tale numero di percorsi di $n$ passi per raggiungere la posizione $k$ restando sempre nella metà non negativa si può ricavare mediante la seguente formula: \[\frac{k+1}{n+1}\binom{n+1}{\frac{n-k}{2}},\quad \text{ per }k=0,1,\dots,n,\;\;\text{ e } n-k\text{ pari}.\]

I percorsi che restano sempre dalla parte positiva in una passeggiata di $n$ passi è un sottinsieme di quelli che da 1 arrivano in $x\gt0$, tanti quanti quelli che in $n-1$ passi arrivano in $x\ge;0$ partendo da 0, il cui numero è $$\displaystyle\sum_{x=0}^{n-1} \binom{n-1}{\lfloor\frac{n-1+x}{2}\rfloor}= \begin{cases} 2^{n-2}& n \text{ pari}\\ \frac{2^{n-1}-\binom{n-1}{\frac{n-1}{2}}}{2}+\binom{n-1}{\frac{n-1}{2}}= \frac{2^{n-1}+\binom{n-1}{\frac{n-1}{2}}}{2}& n\text{ dispari}\end{cases}.$$ Da questi occorre escludere quelli che passano ancora per il punto iniziale. Secondo il Principio di Riflessione, il numero di percorsi da $x_1 > 0$ a $x_2 > 0$ che ripassano per il punto iniziale è uguale al numero di tutti i percorsi da $-x_1$ a $x_2$. Allora il numero di percorsi che da 1 raggiungono alla fine $x > 0$ ripassando per il punto iniziale è lo stesso di quelli che da -1 raggiungono alla fine $x\gt0$, ovvero lo stesso di quelli che in $n-1$ passi raggiungono $x\ge2$ partendo da 0, cioè $$\displaystyle\sum_{x=2}^{n-1} \binom{n-1}{\lfloor\frac{n-1+x}{2}\rfloor}= \begin{cases} 2^{n-2}-\binom{n-1}{\frac{n}{2}}& n \text{ pari}\\\frac{2^{n-1}-\binom{n-1}{\frac{n-1}{2}}}{2}& n \text{ dispari}\end{cases}.$$ Quindi il numero di percorsi complessivo che restano sempre dalla parte positiva è $\begin{cases}\binom{n-1}{\frac{n}{2}} & n\text{ pari} \\ \binom{n-1}{\frac{n-1}{2}}& n\text{ dispari}\end{cases}.$
Di conseguenza possiamo dire che il numero di percorsi che non ritornano più all'inizio in una passeggiata casuale di $n$ passi, somma di quanti restano sempre positivi e di quelli che restano sempre negativi, per $n$ pari è $2\binom{n-1}{\frac{n}{2}} = \binom{n-1}{\frac{n}{2}}+\binom{n-1}{\frac{n-1}{2}-1}=\binom{n}{\frac{n}{2}}$ mentre per $n$ dispari risulta $2\binom{n-1}{\frac{n-1}{2}}$.
Per $n$ pari tale numero è lo stesso dei percorsi che terminano nel punto iniziale ma anche quello dei percorsi che si mantengono sempre dallo stesso lato compreso il punto iniziale, già valutati come $\displaystyle\sum_{k=0,\; k\text{ pari}}^n\frac{k+1}{n+1}\binom{n+1}{\frac{n-k}{2}}$. (Random Walks and Catalan Factorization, by E Omer).
Per dimostrare questi risultati possiamo basarci sulla costruzione di biiezioni tra questi diversi insiemi di percorsi.
In primo luogo, descriviamo una biiezione tra percorsi che finiscono nel punto iniziale e percorsi non negativi. Consideriamo come "parte iniziale" di un percorso che finisce nel punto iniziale quella che termina alla prima volta che raggiunge il suo valore minimo. Consideriamo come "parte finale" di un percorso non negativo quella che inizia dall'ultima volta che raggiunge metà del suo valore finale. La biiezione prende la parte iniziale di un percorso che finisce nel punto iniziale, inverte i segni e l'ordine dei passi e lo posiziona alla fine del cammino. La biiezione inversa prende la parte finale di un percorso non negativo, inverte i segni e l'ordine dei passi e lo posiziona all'inizio del cammino.

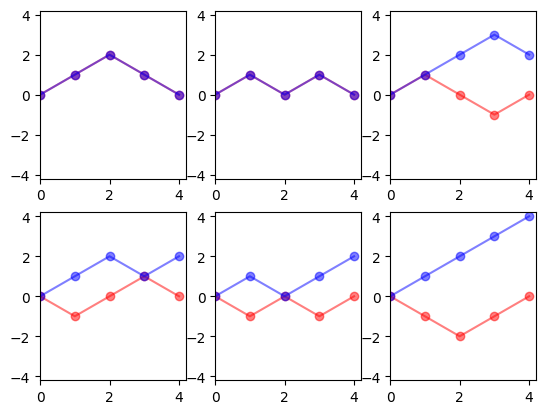
In secondo luogo, descriviamo una biiezione simile tra percorsi che finiscono nel punto iniziale e percorsi non nulli. Consideriamo come "parte iniziale" di un percorso che finisce nel punto iniziale quella che termina alla prima volta che raggiunge il suo valore minimo, per i percorsi che iniziano con un passo verso il basso, o il suo valore massimo, per i percorsi che iniziano con un passo verso l'alto. Si consideri la "parte iniziale" di un percorso diverso da zero fino all'ultima volta che raggiunge metà del suo valore finale, con un passo ascendente, per percorsi positivi, o con un passo discendente, per percorsi negativi. La biiezione e la sua inversa invertono i segni e l'ordine dei passi nelle parti iniziali.

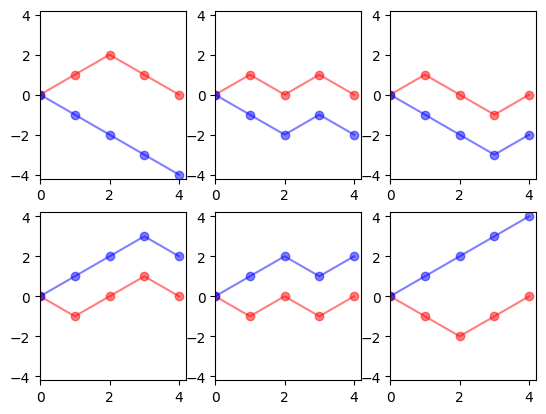
Il numero di percorsi non negativi che ritornano a 0 per la prima volta proprio al tempo $n$ di $n$ passi , ovviamente pari, è \[\frac{1}{n-1}\binom{n}{\frac{n}{2}}\] cioè i numeri di Catalan 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, ... .

Una passeggiata con esattamente $k$ ritorni a 0 è ottenuta concatenando $k$ passeggiate che ritornano a 0 per la prima volta solo alla fine seguite da una passeggiata finale che evita di tornare in 0, quindi il loro numero è \[\sum_{\begin{matrix}n_1, n_2,\dots,n_k\\n_1+n_2+\dots+n_k=n\end{matrix}}\frac{1}{n_1-1}\binom{n_1}{\frac{n_1}{2}}\frac{1}{n_2-1}\binom{n_2}{\frac{n_2}{2}}\dots\frac{1}{n_{k-1}-1}\binom{n_{k-1}}{\frac{n_{k-1}}{2}}\binom{n_k}{\frac{n_k}{2}}\]

La funzione generatrice del numero dei percorsi di $n$ passi che non tornano più a 0 è $$\displaystyle\sum_{n\ge0}\binom{2n}{n}x^n=\frac{1}{\sqrt{1-4x}}$$ mentre $$\displaystyle\sum_{n\ge0}\frac{1}{2n-1}\binom{2n}{n}x^n=1-\sum_{n\ge0}\binom{2n}{n}x^n=1-\frac{1}{\sqrt{1-4x}}$$ è la funzione generatrice di una passeggiata con ritorno a 0 solo alla fine.
Una passeggiata che ha esattamente $k$ ritorni a 0, ottenuta concatenando $k$ passeggiate con unico ritorno a 0 finale seguite da una passeggiata che evita ogni ritorno 0 ha, per il numero di tali passeggiate, come funzione generatrice $$\displaystyle\left(\sum_{n\ge0}\frac{1}{2n-1}\binom{2n}{n}x^n\right)^k\sum_{n\ge0}\binom{2n}{n}x^n=\frac{1}{\sqrt{1-4x}}\left(1-\frac{1}{\sqrt{1-4x}}\right)^.k$$