La letteratura contemporanea si è ormai arricchita delle opere dell'ingegner Carlo Emilio Gadda, del chimico Primo Levi, del logico Bertrand Russell, del geometra Salvatore Quasimodo, del matematico Alexander Solzhenitzin (questi ultimi premi Nobel per la letteratura, rispettivamente nel 1950, 1959 e 1970), oltre che di autori che hanno fatto studi scientifici, quali Robert Musil, Hermann Broch, Friedrich Dürrenmatt, Thomas Pynchon, ... Un'intera corrente letteraria, che va dall'Oulipo (Ouvroir de Littérature Potentielle) francese all'Oplepo (Opificio di Letteratura Potenziale) italiano, ha addirittura assunto la realizzazione di opere a struttura dichiaratamente matematica come sua poetica: ad esso appartenevano autori di primo piano come Raymond Queneau, Georges Perec e Italo Calvino. Infine, la nascita della fantascienza e del cyberpunk come generi autonomi ha colmato un bisogno di tematiche che sono evidentemente al di fuori della portata di autori di formazione umanistica, dai viaggi spaziali ai calcolatori, e ha già portato alla ribalta talenti linguistici di tutto rispetto, da Stanislav Lem a William Gibson.
Anzitutto, essa soddisfa perfettamente alla definizione di Pound della grande letteratura, come ``linguaggio carico di significato al massimo grado''.10 Per il suo simbolismo altamente rarefatto e la sua capacità di condensazione, la matematica svolge nella scienza un ruolo analogo a quello della poesia nell'umanesimo: il diagramma apparentemente lineare poesia ? letteratura ? filosofia ? scienza ? matematica
dello spiegamento espressivo risulta dunque essere in realtà circolare, poichè i suoi apparentemente contrapposti estremi sono in realtà coincidenti, e la sua chiusura individua una vera e propria ruota della vita culturale, in cui tutti i termini finiscono per essere identificati nella loro essenza.
... nella matematica si trovi la cerniera di collegamento fra le due culture, il corpo calloso che collega i due emisferi, il linguaggio poetico della natura, il mediatore neutrale che permette di riappacificare le apparenti discordanze culturali.
da Culture: una, nessuna o centomila? di Piergiorgio Odifreddi, Febbraio 1997

Si potrebbero classificare le attività umane secondo il numero di parole di cui hanno bisogno: più gliene occorrono e più c'è da pensar male del loro carattere
L'uomo senza qualità

«[…] Durante la lezione di matematica, a Törless venne all’improvviso un’idea. Già negli ultimi giorni aveva seguito con particolare interesse le lezioni, pensando: “Se tutto questo costituisce davvero la preparazione alla vita, come dicono, dovrà pur trovarvisi almeno un accenno di ciò che io vado cercando”.
E aveva pensato proprio alla matematica, ancora preso da quei pensieri sull’infinito. E infatti, nel bel mezzo della lezione, aveva avuto una sorta di illuminazione. Appena finita l’ora andò a sedersi accanto a Beinberg, che era l’unico con il quale potesse parlare di cose simili.
“Ehi, tu l’hai capita bene poco fa?”
“Che cosa?”
“La storia dei numeri immaginari”
“Sì. Non è poi così difficile. Bisogna solo ricordare che l’unità di calcolo è data dalla radice quadrata di meno uno.”
“Ma è proprio questo il punto. Quella radice non esiste. Qualsiasi numero, che sia negativo o positivo, elevato al quadrato dà un valore positivo. Per cui non può esserci un numero reale che sia la radice quadrata di qualcosa di negativo.” “Giustissimo; ma perché non si dovrebbe tentare ugualmente di applicare l’operazione di estrazione della radice quadrata anche a un numero negativo? Naturalmente questo non potrà dare alcun valore reale, e infatti anche per questo il risultato è detto immaginario. E’ come se si dicesse: qui di solito si siede sempre un tale, perciò mettiamogli anche oggi una seggiola; e se anche fosse morto nel frattempo, facciamo come se venisse.”
“Ma come si può se si sa con certezza, con matematica certezza, che è impossibile?” “Appunto, si fa come se fosse possibile. Un qualche risultato ne uscirà. In fondo, con i numeri irrazionali non è la stessa cosa? Una divisione che non finisce mai, una frazione il cui valore non risulterà mai e poi mai per quanto tu continui a calcolare. E che mi dici, poi, del fatto che due parallele si devono incontrare all’infinito? Io credo che a essere troppo scrupolosi la matematica finirebbe per non esistere più.”
“Questo è vero. Se uno se l’immagina così, è davvero bizzarra. Ma la cosa singolare è proprio che ciononostante con quei valori immaginari o comunque impossibili si possano fare calcoli perfettamente reali e raggiungere alla fine un risultato concreto!”
“Beh, per arrivare a questo i fattori immaginari devono elidersi a vicenda durante il calcolo.”
“Sì, sì, tutto quello che dici lo so anch’io. Ma pure non resta un che di curioso in tutta la faccenda? Come posso spiegarmi? Prova a pensarla così: in un calcolo del genere, tu hai all’inizio dei numeri solidissimi, in grado di quantificare metri, pesi o qualsiasi altro oggetto concreto, comunque numeri reali. Alla fine del calcolo, lo stesso. Ma l’inizio e la fine sono tenuti insieme da qualcosa che non c’è. Non è un po’ come un ponte che consti soltanto dei piloni iniziali e finali, e sul quale tuttavia si cammina sicuri come se fosse intero? Un calcolo del genere mi dà il capogiro; come se un pezzo del cammino andasse Dio sa dove. Ma la cosa davvero inquietante per me è la forza insita in questi calcoli, una forza capace di sorreggerti fino a farti arrivare felicemente dall’altra parte.” Beineberg ghignò: “Parli già quasi come il prete: “…Tu vedi una mela- e sono le oscillazioni della luce, è l’occhio eccetera -, e allora allunghi la mano per rubarla- e sono i muscoli e i nervi che la fanno muovere. Ma tra l’una e l’altra azione vi è qualcosa che fa nascere l’una dall’altra- ed è l’anima immortale, che qui ha peccato… Già già, nessuna delle vostre azioni è spiegabile senza l’anima, la quale vi suona come foste tasti di un pianoforte…” ”. E imitò la cadenza con la quale il sacerdote era solito raccontare questa antica parabola. “Peraltro, tutta questa storia non mi interessa un gran che.”
“Io invece pensavo che dovesse interessarti, e molto. Perlomeno, io non ho potuto non pensare subito a te, perché questo- se è davvero così inspiegabile- sarebbe quasi una conferma di quello a cui credi tu.”
“Perché non dovrebb’essere inspiegabile? Ritengo possibilissimo che gli inventori della matematica si siano fatti lo sgambetto da soli. Infatti, ciò che sta al di là del nostro intelletto non potrebbe essersi voluto prendere gioco di quello stesso intelletto? Ma in queste cose io non mi ci metto, non portano a un bel nulla. […]»
da "I turbamenti del giovane Törless"

Tre casi di studio: Carroll, Calvino e Borges, di Piergiorgio Odifreddi

Bisogna evitare, disse Triuscaillon, che, in questa semplice ellisse si utilizzi iperbolicamente il circolo vizioso della parabola.
Zazie dans le métro

Non esiste un solo mondo, quello che lei vede o che crede di vedere, o che immagina di vedere o che vuole vedere, quel mondo che toccano i ciechi, sentono i mutilati e annusano i sordi, quel mondo di cose e di forze, di solidità o di illusioni, di vita e di morte, di nascita e di distruzioni, il mondo in cui viviamo, in mezzo al quale siamo soliti addormentarci. Per quel che ne so io, ne esiste almeno un altro: quello dei numeri e delle figure, delle identità e delle funzioni, delle operazioni e dei gruppi, degli insiemi e degli spazi. C'è gente, come sa, che pretende si tratti solo di astrazioni, costruzioni, combinazioni. Vogliono far credere a una specie di architettura; si prendono degli elementi nella natura, si affinano, si puliscono, si prosciugano e lo spirito umano costruisce con questi mattoni, una casa splendida, magistrale testimonianza della potenza della sua ragione. Dovete certamente conoscere questa teoria, il vostro professore di filosofia l'avrà sostenuta: è la più volgare che ci sia. Un fabbricato, considerano la scienza matematica un fabbricato! Ci si assicura della solidità delle fondamenta prima di costruire il pianterreno si passa al primo piano poi al secondo e così di seguito senza che ci sia motivo di interruzione. Ma in realtà le cose non vanno così; non all'architettura, all'edilizia bisogna paragonare la geometria o l'analisi,ma alla botanica,alla geografia, alle scienze fisiche. Si tratta di descrivere un mondo, di scoprirlo e non di costruirlo o inventarlo, perché esiste al di fuori dello spirito umano e indipendente da esso. Dobbiamo esplorare quest'universo e dire poi agli uomini quel che ci abbiamo visto. Ma per esprimerlo, occorre un linguaggio: quello dei segni e delle formule, quello che si considera comunemente l'essenza stessa della scienza e non ne è che il modo d'espressione. Questo linguaggio si rivela ancor più impotente a descrivere le ricchezze del mondo matematico che non la lingua francese a formulare la molteplicità delle cose, poiché esse non si situano allo stesso livello d'esistenza.
Odile

consiste nel raccontare 99 volte in 99 diversi stili letterari e non solo, lo stesso banale fatto di un giovane dal lungo collo che litiga sull'autobus e che successivamente incontra un amico. Almeno due di questi racconti sono narrati da un punto di vista matematico.

 

Visione insiemistica.
Nell'autobus S consideriamo l'insieme A dei viaggiatori seduti e l'insieme D dei viaggiatori in piedi. Ad una certa fermata vi è l'insieme P delle persone che aspettano. Sia C l'insieme dei viaggiatori che salgono; questo è un sottoinsieme di P ed è anche l'unione di C', insieme dei viaggiatori che restano sulla piattaforma, con C" , insieme di quelli che vanno a sedersi. Dimostrare che C" è vuoto.

 

Sia Z l'insieme dei giovinastri e {z} l'intersezione di Z con C', ridotto a un solo elemento. In seguito alla suriezione dei piedi di z su quelli di y (elemento qualunque di C' diverso da z), si crea un insieme M di parole pronunciate da z. Essendo adesso l'insieme C" non vuoto, dimostrare che è formato dal solo z.

 

Sia adesso P l'insieme dei pedoni che si trovano dinanzi la Gare Saint Lazare, {z, z'}, l'intersezione di Z con P, B l'insieme dei bottoni del soprabito di z, B' l'insieme dei possibili spostamenti dei sopradetti bottoni secondo z', dimostrare che l'iniezione di B in B' non è una biiezione.

 

Visione geometrica.
In un parallelepipedo rettangolo si tracci la retta di equazione 84x + S = y; un omoide A che, al di sopra di una parte cilindrica di lunghezza l > n, porta una calotta sferica circondata da due sinusoidi, presenta un punto di contatto con un omoide banale B. Dimostrare che questo punto di contatto è un punto di arruffamento.

 

Se l'omoide A incontra un omoide omologo C, allora il punto di contatto è un disco di raggio r < l. Determinare l'altezza h di questo punto di contatto in rapporto all'asse verticale dell'omoide A.
Exercices de style

La vita istruzioni per l'uso

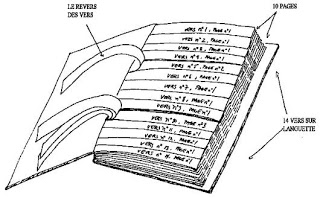
di Georges Perec.

È costruito sopra un quadrato greco-latino 10x10 rappresentato nella pagina l'immeuble, e le sue caselle corrispondono alle stanze del condominio parigino (e quindi ai 99 capitoli del romanzo ognuno dei quali rappresenta l'istantanea di una stanza del condominio di dieci piani).
Nella pagina dedicata ai contraintes (vincoli) sono riportati i 42 elenchi di 10 elementi ciascuno che Perec compose per utilizzarli come "vincoli narrativi". Come potete vedere, ci sono due elenchi di autori che possono essere citati (citation 1 e citation 2), un elenco di epoche (époque), uno di animali (animaux), uno di sentimenti (sentiments), e così via. In ognuno degli elenchi gli elementi sono identificati dalle lettere a, b, c, ..., j.
Ogni elenco è contrassegnato da un codice, riportato nella colonna id e formato da una lettera (A oppure B oppure C) e da una cifra (da 0 a 9). Se trascuriamo la differenza tra lettere maiuscole e minuscole, gli elenchi risultano riuniti in 21 coppie: ad esempio, i primi due elenchi, rispettivamente contenenti posizioni (position) e attività (activité), sono accoppiati e contrassegnati dal codice 1A/1a.
da Il grande quadrato di Perec di Paolo Alessandrini