Non c'è dubbio che, per quanto semplice possa sembrare, il moto browniano è uno dei modelli fondamentali del calcolo stocastico.
Un moto browniano scalare standard, o processo di Wiener standard, su $[0, T]$ è una variabile casuale $W(t)$ che dipende con continuità da $t \in [0, T]$ e soddisfa le seguenti tre condizioni:
- $W(0) = 0$ (con probabilità 1).
- Per $0 < s < t < T$ la variabile casuale data dall'incremento $W(t) - W(s)$ è normalmente distribuita con media zero e varianza $t - s$; equivalentemente, $W(t) -W(s) =\sqrt{t - s} N(0, 1)$, dove $N(O, 1)$ denota una variabile casuale normalmente distribuita con media zero e varianza unitaria.
- Per $0 < s < t < u < v < T$ gli incrementi $W(t) - W(s)$ e $W(v) - W(u)$ sono indipendenti.
Per realizzare una simulazione in Python senza ricorrere a librerie se non numpy.random che rende disponibili diversi generatori di numeri casuali per vari processi casuali. In particolare numpy.random.randn() fornisce numeri a caso secondo la distribuzione normale con media zero e varianza unitaria.
import numpy as np
import matplotlib.pyplot as plt
plt.hist(np.random.randn(1000), density = True, bins = 16 );
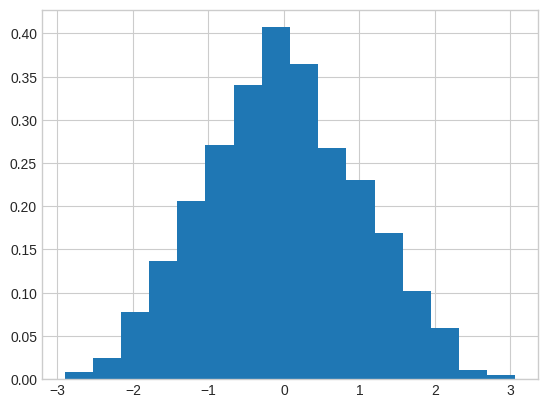
Il moto browniano non è altro che la somma cumulativa di valori casuali normalmente distribuiti con media zero e varianza $\Delta t$.
T, N = 1, 500
dt = float(T)/N
t = np.linspace(0,T,N+1)
dW = np.sqrt(dt)*np.random.randn(N)
W = np.append([0],np.cumsum(dW));
fig = plt.figure(figsize=(10,5))
plt.plot(t,W)
plt.xlabel(r'$t$',fontsize=14)
plt.ylabel(r'$W(t)$',fontsize=14,rotation=0)
plt.title('A Brownian motion')
plt.show()
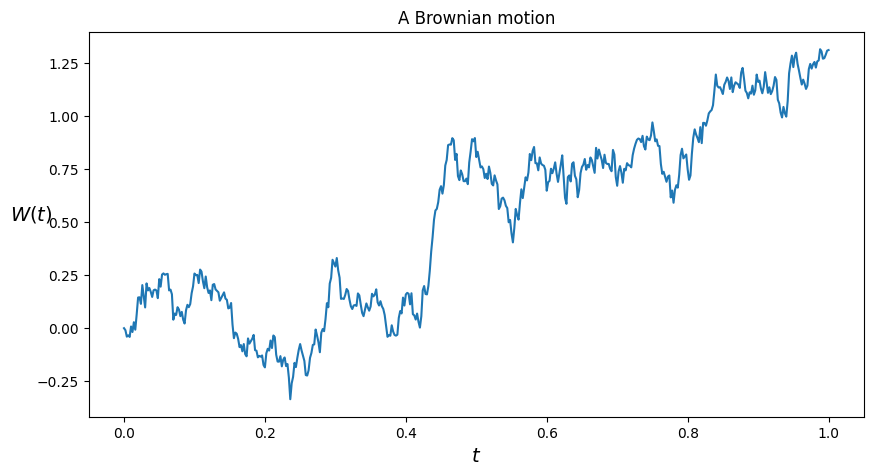
Si possono realizzare più simulazioni e il loro valore medio.
T, N = 1, 500
dt = float(T)/N
t = np.linspace(0,T,N+1)
M = 1000
dW = np.sqrt(dt)*np.random.randn(M,N)
W = np.cumsum(dW,axis=1)
W_mean = np.mean(W,axis=0)
fig = plt.figure(figsize=(10,5))
plt.plot(t[1:],W_mean)
for i in range(5):
plt.plot(t[1:],W[i,:], 'r--')
plt.legend((f'mean of {M} paths', '5 individual paths'),loc=2,shadow=True)
plt.xlabel('$t$',fontsize=14)
plt.ylabel('$W(t)$',fontsize=14,rotation=0)
plt.show()
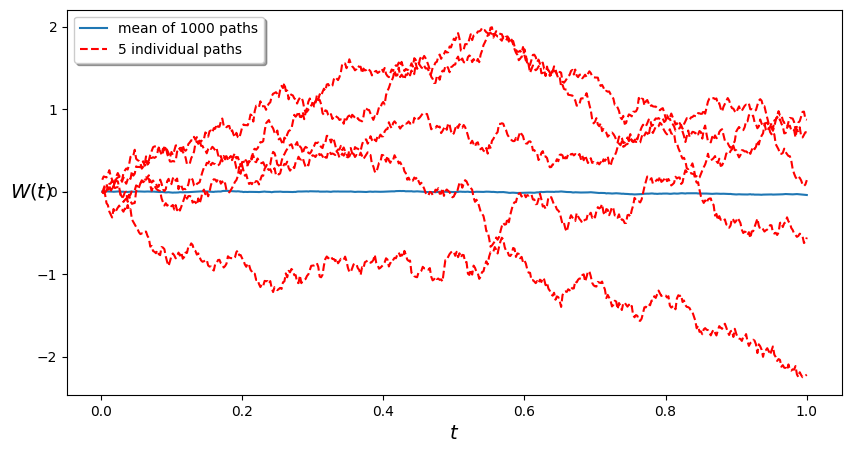
Molti modelli statistici e fisici vengono costruiti manipolando i percorsi browniani.
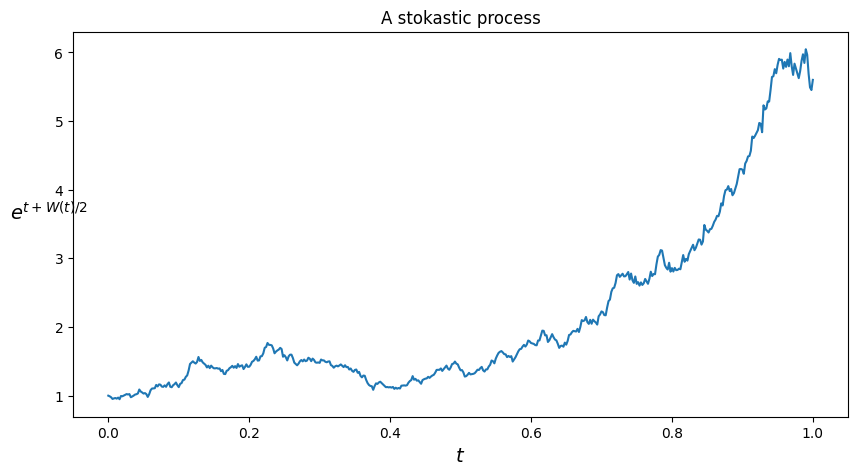
Ad esempio trasformiamo i percorsi browniani simulati tramite una funzione definita dall'utente come $e^{t+\frac{1}{2}W(t)}$.
T, N = 1, 500
dt = float(T)/N
t = np.linspace(0,T,N+1)
dW = np.sqrt(dt)*np.random.randn(N)
W = np.append([0],np.cumsum(dW));
U = np.exp(t+0.5*W)
fig = plt.figure(figsize=(10,5))
plt.plot(t,U)
plt.xlabel(r'$t$',fontsize=14)
plt.ylabel(r'$e^{t+W(t)/2}$',fontsize=14,rotation=0)
plt.title('A stokastic process')
plt.show()
Si possono realizzare più simulazioni e il loro valore medio.
T, N = 1, 500
dt = float(T)/N
t = np.linspace(0,T,N+1)
M = 1000
dW = np.sqrt(dt)*np.random.randn(M,N)
W = np.cumsum(dW,1)
U = np.exp(np.tile(t[1:],(M,1))+0.5*W)
U_mean = np.append([1],np.mean(U,axis=0))
fig = plt.figure(figsize=(10,5))
plt.plot(t,U_mean)
for i in range(5):
plt.plot(t,np.concatenate(([1,],U[i,:])), 'r--')
plt.legend((f'mean of {M} paths', '5 individual paths'),loc=2,shadow=True)
plt.xlabel('$t$',fontsize=14)
plt.ylabel('$U(t)$',fontsize=14,rotation=0)
plt.show()
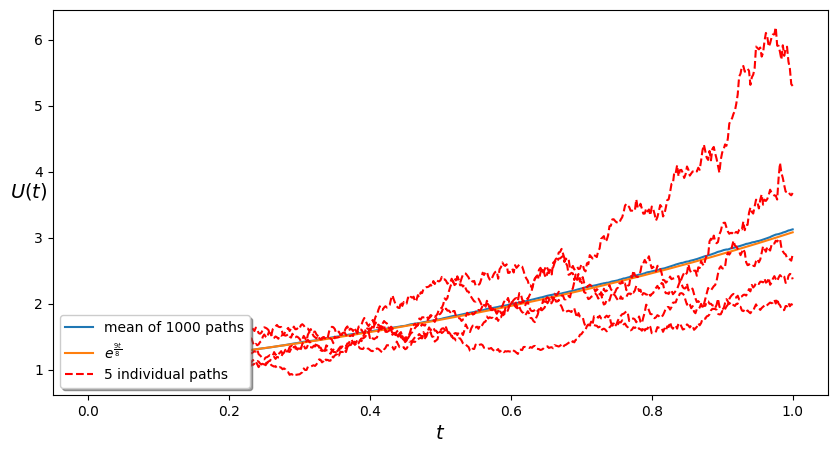
Sebbene $U(W(t))$ non sia regolare lungo i singoli percorsi, la sua media campionaria appare regolare. Per questa funzione, possiamo effettivamente calcolare analiticamente il valore atteso in ogni istante: $e^\frac{9t}{8}$. Infatti $t+\frac{1}{2}W(t)\sim N(t,t/4)$ e $e^{N(t,t/4)} \sim log N (t,t/4)$.
Possiamo servirci della libreria sdeint che, innanzitutto, dovrà essere installata.
!pip install sdeint
La libreria fornisce in particolare un metodo per produrre una serie di $dW$.
plt.plot(range(100),sdeint.deltaW(100, 1, 0.01, generator=None))
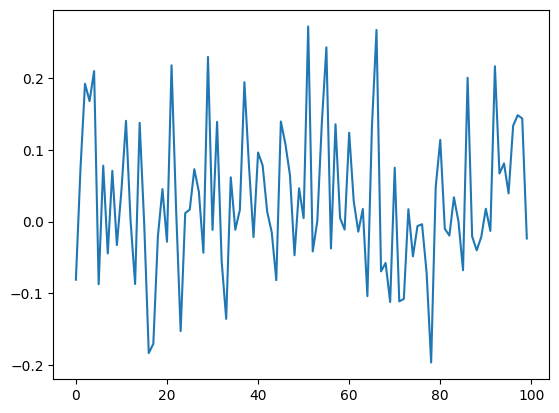
Quindi si può simulare un cammino browniano.
import sdeint
plt.plot(range(100),sdeint.deltaW(100, 1, 0.01, generator=None).cumsum())
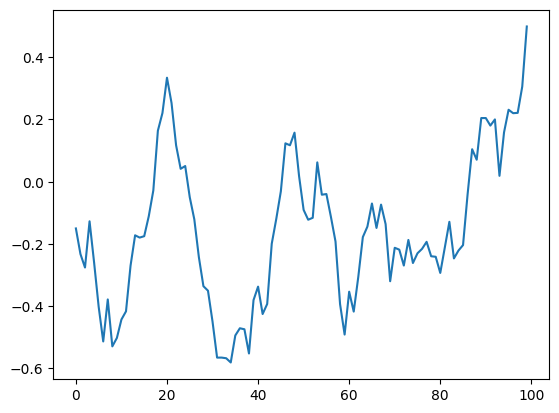
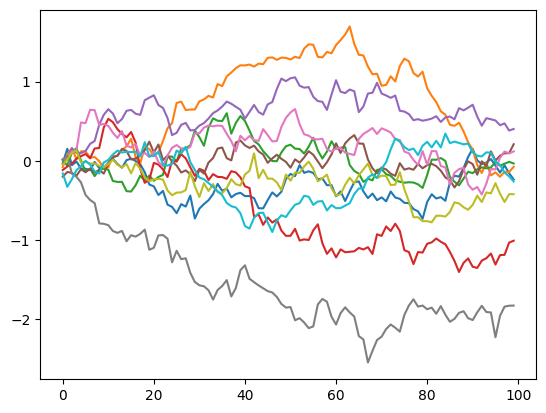
Si possono simulare diversi cammini browniani.
L, N = 100, 10
Wi = sdeint.deltaW(L, N, 0.01, generator=None).cumsum(axis=0)
for i in range(N):
plt.plot(range(L),Wi[:, i])
- Stochastic simulation , From Wikipedia, the free encyclopedia
- Passeggiate casuali in questo sito