La soluzione approssimata ottenuta con il metodo Euler-Maruyama corrisponde più fedelmente alla soluzione vera man mano che $\Delta t$ diminuisce, sembra cioè che si verifichi la convergenza.
Tenendo presente che $X(\tau_n)$ e $X_n$ sono variabili casuali, per rendere precisa la nozione di convergenza dobbiamo decidere come misurare la loro differenza. Utilizzando il valore atteso $\mathbb E|X_n - X(\tau_n)|$, si arriva al concetto di convergenza forte. Si dice che il metodo ha ordine di convergenza forte pari a $\gamma$ se esiste una costante $C$ tale che \[\mathbb E|X_n - X(\tau_n)|< C\Delta t^\gamma, \] per ogni fissato $\tau_n = n\Delta t\in [0, T]$, e per $\Delta t$ sufficientemente piccolo.
Se $f$ e $g$ soddisfano le condizioni appropriate, si può dimostrare che il metodo Euler-Maruyama ha un ordine di convergenza forte $\gamma = 2$.
Si noti che questo segna un allontanamento dall'impostazione deterministica: se $g = 0$ e $X_0$ è costante, allora $\mathbb E|X_n - X(\tau_n)|=X_n - X(\tau_n)< C\Delta t$ e la disuguaglianza è vera con $\gamma = 1$.

Nei test numerici che seguono ci concentriamo sull'errore all'estremo $t = T$, quindi indichiamo \[e^{strong}_{\Delta t}= \mathbb E|X_L - X(T)|,\quad \text{dove } L\Delta t = T,\] l'errore all'estremo in questo senso forte. Se il limite è valido con $\gamma=\frac{1}{2}$ in qualsiasi punto fisso in $[0, T]$, allora è certamente valido all'estremo, quindi abbiamo \[e^{strong}_{\Delta t} < C\Delta t^\frac{1}{2}\] per $\Delta t$ sufficientemente piccolo.

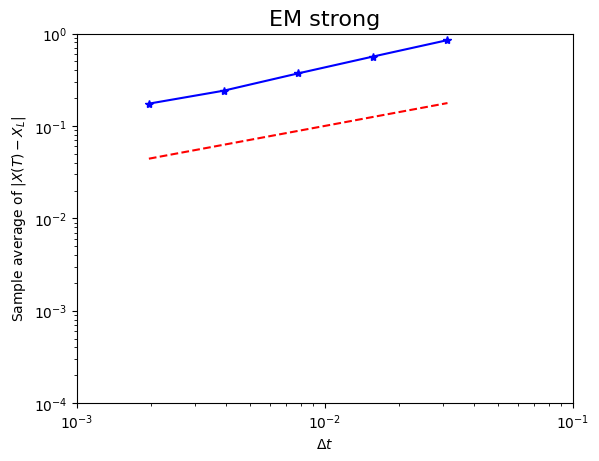
Si esamina qui la convergenza forte di EM per l'SDE lineare utilizzando gli stessi $\lambda$, $\mu$ e $X_0$ già precedentemente utilizzati. Calcoliamo M diversi cammini browniani discretizzati su $[0, 1]$ con $δt = 2^{-9}$. Per ogni percorso, EM viene applicato con 5 diverse dimensioni di passo: $Δt = 2^pδt$ per $p=0,1,2,3,4$. L'errore finale nel s-esimo percorso campione, con $s=0,1,\dots, M-1$, per il p-esimo passo è memorizzato in Xerr(s,p); quindi Xerr è un array Mx5.
Il metodo numpy.mean() viene quindi utilizzata per calcolare la media su tutti i percorsi campione: mean(Xerr) produce un array 1x5 in cui ogni colonna di Xerr viene sostituita dalla sua media. Quindi il p-esimo elemento di mean(Xerr) è un'approssimazione di $e^{strong}_{\Delta t}$ per $Δt = 2^pδt$.
Se la disuguaglianza è verificata con uguaglianza approssimativa, allora, prendendo i logaritmi, $\log e^{strong}_{\Delta t} < \log C+ \frac{1}{2}\log\Delta t$.
Il comando loglog(Δtvals ,mean (Xerr), 'b*-') traccia la nostra approssimazione di $e^{strong}_{\Delta t}$ rispetto a $Δt$ su una scala logaritmica. Questo produce gli asterischi blu collegati con linee continue nel grafico. Aggiunta come riferimento una linea rossa tratteggiata con pendenza pari a $\frac{1}{2}$, osserviamo che le pendenze delle due curve sembrano corrispondere bene, suggerendo che la relazione di convergenza forte per $\gamma=\frac{1}{2}$ è valida.

Monitorando l'errore $e^{strong}_{\Delta t}$ assumiamo implicitamente che alcune altre fonti di errore siano trascurabili, tra cui

• l'errore derivante dall'approssimazione di un valore atteso tramite una media campionata (Errore di campionamento),
• gli errori intrinseci nel generatore di numeri casuali (Bias dei numeri casuali),
• gli errori di arrotondamento in virgola mobile (Errori di arrotondamento).

Si dice che un metodo ha ordine di convergenza debole pari a $\gamma$ se esiste una costante $C$ tale che per tutte le funzioni $p$ in una certa classe \[|Ep(X_n) - Ep(X(\tau))| \le C\Delta t^\gamma\] per qualsiasi $\tau = n\Delta t\in[0, T]$ e $\Delta t$ sufficientemente piccolo. Tipicamente, le funzioni $p$ devono soddisfare le condizioni di regolarità e crescita polinomiale. Ci concentreremo sul caso in cui $p$ è la funzione identità. Per $f$ e $g$ appropriate si può dimostrare che EM ha ordine di convergenza debole $\gamma = 1$.
Imitando i nostri test di convergenza forte, poniamo \[e^{weak}_{\Delta t} = |\mathbb E X_L - \mathbb EX(T)|, \quad \text{dove } L\Delta t = T,\] per denotare l'errore debole del punto finale in EM. Quindi per $p(X) = X$ e con $\gamma = 1$ ciò implica che \[e^{weak}_{\Delta t} \le C\Delta t\] per $\Delta t$ sufficientemente piccolo.

Campioniamo 50.000 cammini browniani discretizzati e utilizziamo cinque passi $\Delta t = 2^p$ per $-9\le p \lt -4$.

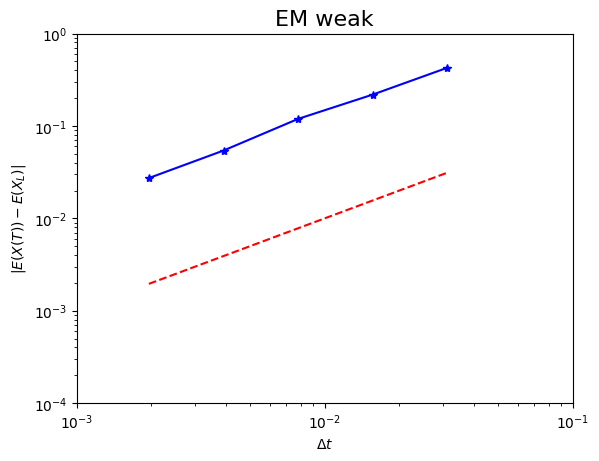
La convergenza debole riguarda solo la media della soluzione, quindi siamo liberi di utilizzare qualsiasi campione $\sqrt{\Delta t}N(O,1)$ per l'incremento $W(\tau_i) - W(\tau_{i-1})$ a qualsiasi passo. Infatti, l'ordine di convergenza debole viene mantenuto se l'incremento viene sostituito da una variabile casuale indipendente a due punti $\sqrt{\Delta t}V_i$, dove $V_i$ assume i valori +1 e -1 con uguale probabilità. (Si noti che $\sqrt{\Delta t}V_i$ ha la stessa media e varianza di $\sqrt{\Delta t}N(O,1)$). Sostituendo l'incremento browniano con $\sqrt{\Delta t}V_i$, in questo modo si ottiene il metodo di Eulero-Maruyama debole, che ha un ordine di convergenza debole $\gamma = 1$, ma, poiché non utilizza informazioni sul percorso, non offre una convergenza forte. La motivazione alla base del metodo di Eulero-Maruyama debole è che i generatori di numeri casuali che campionano da $V_i$ possono essere resi più efficienti di quelli che campionano da $N(0,1)$.