Come l'integrale riemanniano di una funzione $f$ si definisce $\displaystyle\lim_{dt\to 0}\sum_{i=0}^{N-1}f(t_i)(\underbrace{t_{i+1}-t_i}_{dt})$, così per analogia la somma $\displaystyle\sum_{i=0}^{N-1}f(t_i)(\underbrace{W_{i+1}-W_i}_{dW})$ può essere vista come approssimazione dell'integrale stocastico $\displaystyle\int_0^Tf(t)dW(t)$.
Possiamo applicare la formula per calcolare l'integrale stocastico della costante 1.
T, N = 1, 500
dt = float(T)/N
sums = []
for _ in range(10000):
dW = np.sqrt(dt)*np.random.randn(N)
sums.append(np.sum(dW))
plt.hist(sums, density = True, bins = 10 );
np.mean(sums), np.std(sums)
(np.float64(0.00790120995222959), np.float64(0.9883636476427954))
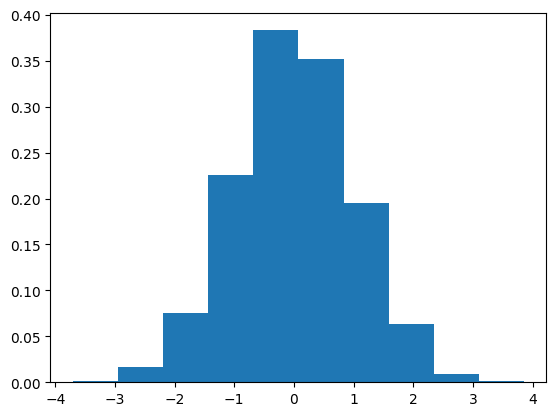
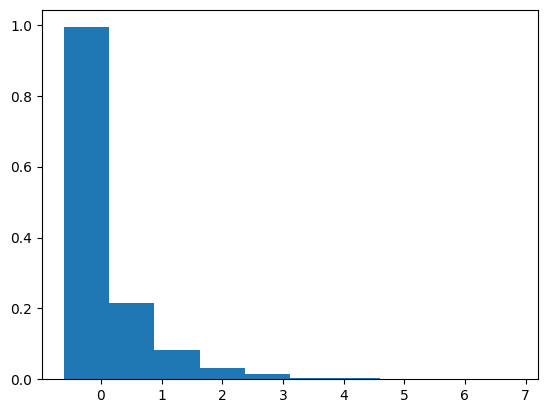
Il risultato è $\displaystyle\lim_{n→∞} \sum_{i=0}^{n-1} 1 ⋅ [W(t_{i+1}) - W(t_i)] = W(t) - W(0) = W(t)=N(0,T)$, semplicemente il processo di Wiener stesso. In generale l'integrale stocastico di una funzione univoca $f(t)$ è $\displaystyle N\left(0,\int_0^T f^2(t)dt\right)$. Possiamo applicare la formula per calcolare l'integrale stocastico di $W(t)$ stesso.
sums = []
for _ in range(10000):
dW = np.sqrt(dt)*np.random.randn(N)
W = np.append([0], np.cumsum(dW))
sums.append(np.sum(W[0:-1]*dW))
plt.hist(sums, density = True, bins = 10 );
np.mean(sums), np.std(sums)
(np.float64(0.008396474620828551), np.float64(0.7115972711321585))
Un modo alternativo per approssimare l'integrale di Riemann è $\displaystyle\sum_{i=0}^{N-1}f\left(\frac{t_i+t_{i+1}}{2}\right)dt$. Così anche $\displaystyle\sum_{i=0}^{N-1}f\left(\frac{t_i+t_{i+1}}{2}\right)dW(t)$ dovrebbe essere approssimazione dell'integrale stocastico.
Nel caso in cui $f(t) = W(t)$, si può dimostrare che $W\left(\frac{t_i+t_{i+1}}{2}\right)$ può sostituirsi con $\frac{W_i+ W_{i+1}}{2}$ incrementato di $N(O, dt/4)$.
sums = []
for _ in range(10000):
dW = np.sqrt(dt)*np.random.randn(N)
W = np.append([0], np.cumsum(dW))
sums.append(np.sum((0.5*(W[0:-1]+W[1:])+0.5*np.sqrt(dt)*np.random.randn(1,N))*dW))
plt.hist(sums, density = True, bins = 10 );
np.mean(sums), np.std(sums)
(np.float64(0.505918832339685), np.float64(0.7057614380562404))
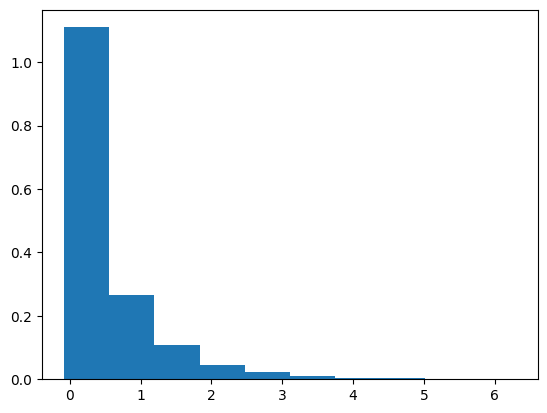
Si noti che le due "somme di Riemann stocastiche" danno risultati diversi anche quando $dt\to 0$.
Si ha così una differenza significativa tra integrazione deterministica e stocastica: nel definire un integrale stocastico come caso limite di una somma di Riemann, dobbiamo essere precisi su come si forma tale somma. La prima dà origine a quello che è noto come integrale Itô, mentre la somma "di punto medio" produce l'integrale di Stratonovich.
La versione di Itô è il caso limite di
$\displaystyle\sum_{i=0}^{N-1}W_i(W_{i+1}-W_i)=\frac{1}{2}\sum_{i=0}^{N-1}\left(W_{i+1}^2-W_i^2-(W_{i+1}-W_i)^2\right)=$
$=\displaystyle\frac{1}{2}\left(W_N^2-W_0^2 - \sum_{i=0}^{N-1}(W_{i+1}-W_i)^2\right)$
da cui, poiché $\displaystyle\sum_{i=0}^{N-1}(W_{i+1}-W_i)^2$ ha valore atteso
$T$ e varianza di $O(dt)$ e per $dt$ piccolo ci aspettiamo che questa variabile casuale
sia vicina alla costante $T$, arriviamo a \[\displaystyle\int_0^TW(t)dW(t)=\frac{1}{2}W^2(T)-\frac{T}{2}\]
per l'integrale di Itô.
Secondo Stratonovich dobbiamo considerare il caso limite per $\displaystyle\sum_{i=0}^{N-1}\left(\frac{W_i+W_{i+1}}{2}+dZ_i\right)(W_{i+1}-W_i)$
dove ogni $dZ_i$ è indipendente $N(0, dt/4)$. Questa somma collassa a
$\displaystyle\frac{1}{2}\left(W_N^2-W_0^2\right)+ \sum_{i=0}^{N-1}dZ_i(W_{i+1}-W_i)$
in cui la sommatoria ha valore atteso nullo e varianza di $O(dt)$. Quindi l'integrale di Stratonovich è
\[\displaystyle\int_0^TW(t)dW(t)=\frac{1}{2}W^2(T).\]
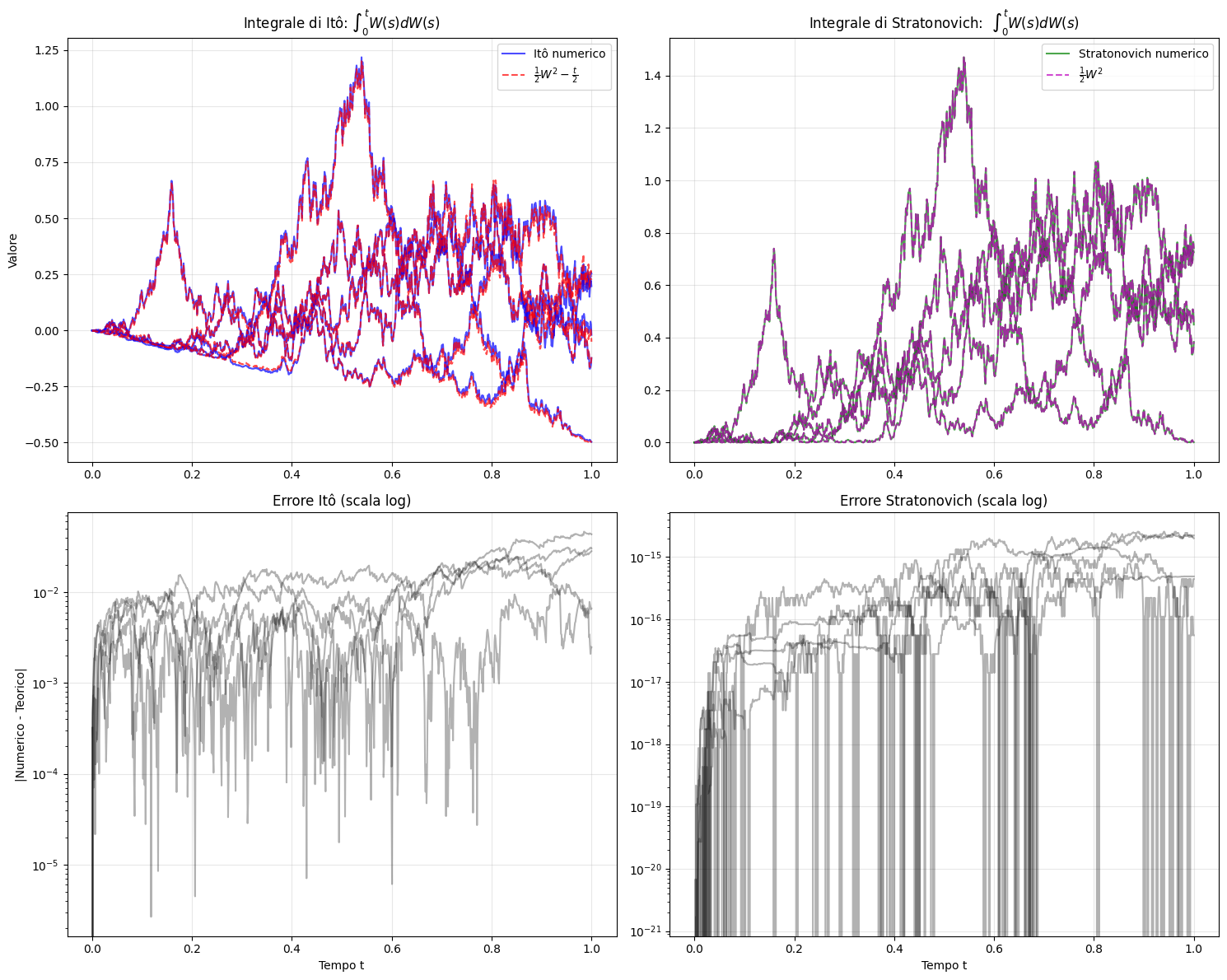
Gli integrali di Ito e Stratonovich hanno entrambi la loro utilità nei modelli matematici.
def verify_w_integral(T=1.0, n_steps=1000, n_paths=5):
"""Verifica numericamente l'integrale stocastico di W(t)"""
t = np.linspace(0, T, n_steps)
dt = t[1] - t[0]
fig, axes = plt.subplots(2, 2, figsize=(15, 12))
for path_idx in range(n_paths):
# Genera un cammino browniano
dW = np.random.normal(0, np.sqrt(dt), n_steps-1)
W = np.zeros(n_steps)
for i in range(1, n_steps):
W[i] = W[i-1] + dW[i-1]
# Calcola l'integrale di Itô di W(t)
ito_integral = np.zeros(n_steps)
for i in range(1, n_steps):
ito_integral[i] = ito_integral[i-1] + W[i-1] * dW[i-1]
# Calcola il risultato teorico: (1/2)W(t)² - (1/2)t
theoretical_ito = 0.5 * W**2 - 0.5 * t
# Calcola l'integrale di Stratonovich (approssimazione)
strato_integral = np.zeros(n_steps)
for i in range(1, n_steps):
# Punto medio per Stratonovich
W_mid = (W[i-1] + W[i])/2
strato_integral[i] = strato_integral[i-1] + W_mid * dW[i-1]
theoretical_strato = 0.5 * W**2
# Plot Itô
axes[0,0].plot(t, ito_integral, 'b-', alpha=0.7,
label='Itô numerico' if path_idx == 0 else "")
axes[0,0].plot(t, theoretical_ito, 'r--', alpha=0.7,
label=r'$\frac{1}{2}W^2 - \frac{t}{2}$' if path_idx == 0 else "")
# Plot Stratonovich
axes[0,1].plot(t, strato_integral, 'g-', alpha=0.7,
label='Stratonovich numerico' if path_idx == 0 else "")
axes[0,1].plot(t, theoretical_strato, 'm--', alpha=0.7,
label=r'$\frac{1}{2}W^2$' if path_idx == 0 else "")
# Differenze
axes[1,0].plot(t, np.abs(ito_integral - theoretical_ito), 'k-', alpha=0.3)
axes[1,1].plot(t, np.abs(strato_integral - theoretical_strato), 'k-', alpha=0.3)
axes[0,0].set_title(r'Integrale di Itô: $\int_0^t W(s) dW(s)$')
axes[0,0].set_ylabel('Valore')
axes[0,0].legend()
axes[0,0].grid(True, alpha=0.3)
axes[0,1].set_title(r'Integrale di Stratonovich: $\int_0^t W(s) dW(s)$')
axes[0,1].legend()
axes[0,1].grid(True, alpha=0.3)
axes[1,0].set_title('Errore Itô (scala log)')
axes[1,0].set_ylabel('|Numerico - Teorico|')
axes[1,0].set_xlabel('Tempo t')
axes[1,0].set_yscale('log')
axes[1,0].grid(True, alpha=0.3)
axes[1,1].set_title('Errore Stratonovich (scala log)')
axes[1,1].set_xlabel('Tempo t')
axes[1,1].set_yscale('log')
axes[1,1].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# Verifica numerica
verify_w_integral()
- Itô calculus, From Wikipedia, the free encyclopedia
- Stratonovich integral, From Wikipedia, the free encyclopedia
- Numerical integration of Ito or Stratonovich SDEs, by Matthew Aburn, Yoav Ram