Un'equazione differenziale scalare può essere scritta in forma integrale come:
\[\displaystyle X(t) = X_0 + \int_0^t f(X(s)) ds +\int_0^t g(X(s)) dW(s), \quad 0 < t < T.\]
Qui, $f$ e $g$ sono funzioni scalari e la condizione iniziale $X_0$ è una variabile casuale.
Assumiamo che il secondo integrale, considerato rispetto al
moto browniano, utilizzi la versione Itô.
La soluzione $X(t)$ è una variabile casuale per ogni $t$.
Seguendo un metodo numerico per risolverla, possiamo quindi considerare la soluzione $X(t)$ come
la variabile casuale che si presenta quando consideriamo il limite di passo nullo nel metodo numerico.
Di solito l'equazione si riscrive in forma differenziale come
\[dX(t) = f(X(t))dt + g(X(t))dW(t),\quad X(0)= X_0,\quad 0 < t < T.\]
Si noti che non ci è consentito scrivere $\frac{dW}{dt}(t)$ poiché il moto browniano
è in ogni punto, certamente, non differenziabile. Teniamo inoltre presente che i tipici teoremi di esistenza
e unicità (e i teoremi di convergenza per i metodi numerici) impongono su $f$ e $g$
vincoli molto più stringenti rispetto alle loro controparti deterministiche.
Per applicare un metodo numerico su $[0, T]$, suddividiamo prima l'intervallo. Sia $\Delta t = \frac{T}{L}$ per un intero positivo $L$, e $\tau_i = i\cdot \Delta t$. Posto $X_i=X(\tau_i)$, il metodo di Eulero-Maruyama assume la forma \[ X_i = X_{i-1} + f(X_{i-1})\Delta t + g(X_{i-1}) (W(\tau_i) - W(\tau_{i-1})),\quad i = 1,2,\dots,L.\]
Per generare gli incrementi $W(\tau_i) - W(\tau_{i-1})$ dei moti browniani discretizzati necessari scegliamo sempre che il passo $\Delta t$ per il metodo numerico sia un multiplo intero $R > 1$ dell'incremento $\delta t$ per il cammino browniano. Questo garantisce che l'insieme di punti $\{t_i\}$ su cui si basa il cammino browniano discretizzato contenga i punti $\{\tau_i\}$ in cui viene calcolata la soluzione aprossimata Eulero-Maruyama. In alcune applicazioni, il cammino browniano è specificato come parte dei dati del problema. Se viene fornito un cammino analitico, è possibile utilizzare un $\Delta t$ arbitrariamente piccolo.
Applichiamo il metodo ad esempio all'equazione differenziale stocastica lineare \[dX(t) = \lambda X(t)dt + \mu X(t)dW(t), X(0) = X_0,\] dove $\lambda$ e $\mu$ sono costanti reali; quindi $f(X) = \lambda X$ e $g(X) = \mu X$. Questa SDE nasce, ad esempio, come modello di prezzo delle attività nella matematica finanziaria. In effetti, la nota equazione differenziale parziale di Black-Scholes ha questa forma e la sua soluzione esatta è \[X(t) = X(0) e^{(\lambda - \frac{1}{2}\mu^2)t+\mu W(t)}. \]
λ=2; μ=1; Xo=1
T=1; N=2**8; δt = float(T)/N
t = np.linspace(0,T,N+1)
dW = np.sqrt(δt)*np.random.randn(1,N)
W = np.cumsum(dW)
Xtrue = Xo*np.exp((λ-0.5*μ**2)*t[1:]+μ*W)
Xtrue = np.insert(Xtrue,0,Xo)
ax=plt.subplot(111)
ax.plot(t,Xtrue)
R=4; Δt=R*δt; L=float(N)/R
Xem = [0]*(int(L)+1)
Xem[0] = Xo
for j in range(1,int(L)+1):
ΔW = np.sum(dW[0][range(R*(j-1),R*j)])
Xem[j] = Xem[j-1] + λ*Xem[j-1]*Δt + μ*Xem[j-1]*ΔW
print( "Error at endpoint: ", np.abs(Xem[-1]-Xtrue[-1]))
ax.plot(np.linspace(0,T,int(L+1)),Xem,'r--*')
ax.legend(("exact","EM"),loc=2)
plt.show()
Error at endpoint: 1.8580400104525836
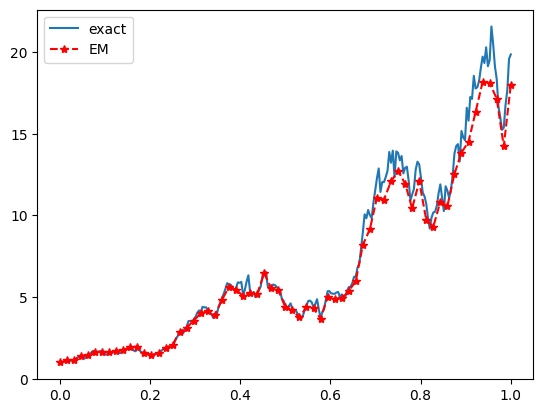
La discrepanza tra la soluzione esatta e la soluzione approssimata al punto finale $t = T$ per $R=4$ è risultata pari a 1.8580400104525836.
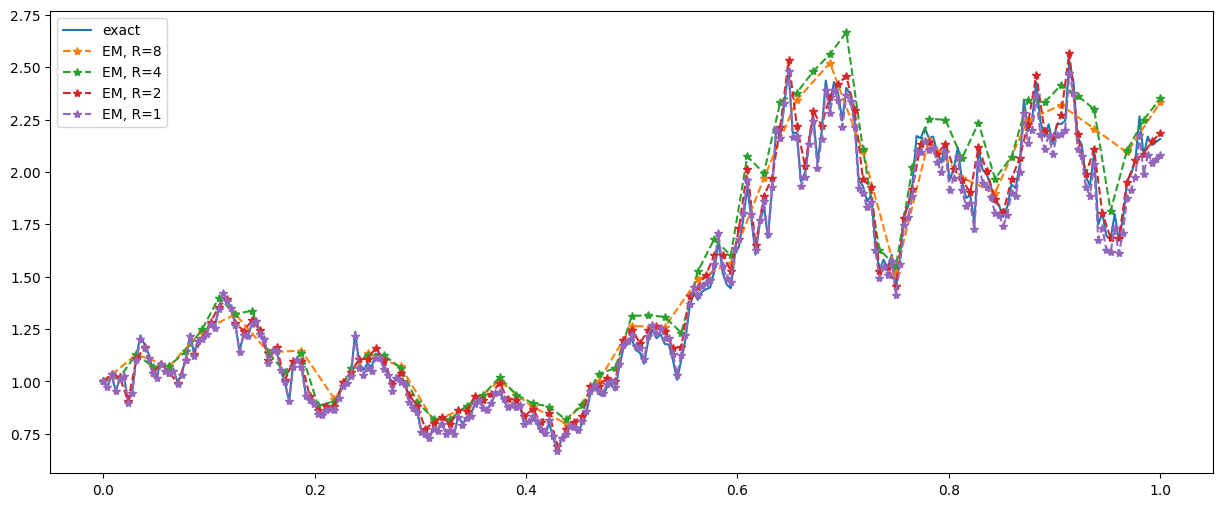
Si possono considerare $\Delta t = R\delta t$ con alcuni altri valori per $R$.
λ=2; μ=1; Xo=1
T=1; N=2**8; δt = float(T)/N
t = np.linspace(0,T,N+1)
dW = np.sqrt(δt)*np.random.randn(1,N)
W = np.cumsum(dW)
Xtrue = Xo*np.exp((λ-0.5*μ**2)*t[1:]+μ*W)
Xtrue = np.insert(Xtrue,0,Xo)
fig, ax = plt.subplots(figsize=(15,6))
ax=plt.subplot(111)
ax.plot(t,Xtrue, label="exact")
for R in [8,4,2,1]:
Δt=R*δt; L=float(N)/R
Xem = [0]*(int(L)+1)
Xem[0] = Xo
for j in range(1,int(L)+1):
ΔW = np.sum(dW[0][range(R*(j-1),R*j)])
Xem[j] = Xem[j-1] + λ*Xem[j-1]*Δt + μ*Xem[j-1]*ΔW
print( f"Error at endpoint (R={R}):", np.abs(Xem[-1]-Xtrue[-1]))
ax.plot(np.linspace(0,T,int(L+1)),Xem,'--*',label=f"EM, R={R}")
plt.legend()
plt.show()
Error at endpoint (R=8): 0.17460482165056312
Error at endpoint (R=4): 0.19325046677254631
Error at endpoint (R=2): 0.026480140826139476
Error at endpoint (R=1): 0.07712633170514671
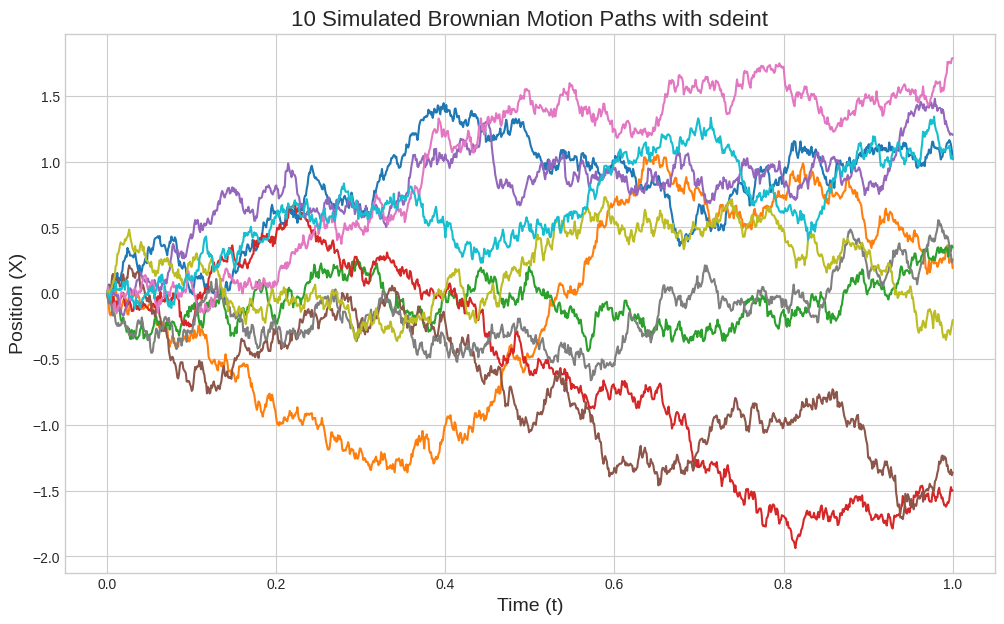
Possiamo utilizzare il metodo .itoint() della libreria sdeint per produrre ad esempio moti browniani come soluzione dell'equazione per $f(X(t))=0,\;g(X(t))=1$.
def f(x, t):
"""Drift function (zero for Brownian motion)."""
return 0
def g(x, t):
"""Diffusion function (constant for standard Brownian motion)."""
return 1
# Set Simulation Parameters
tspan = np.linspace(0.0, 1.0, 1001) # Time vector
x0 = 0.0 # Initial value
npaths = 10 # Number of paths to simulate
# Run the Simulation in a Loop and Plot
plt.style.use('seaborn-v0_8-whitegrid')
plt.figure(figsize=(12, 7))
# Loop to generate and plot each path
for i in range(npaths):
# The correct function is sdeint.itoint
result = sdeint.itoint(f, g, x0, tspan)
plt.plot(tspan, result)
# Add Labels and Title
plt.xlabel("Time (t)", fontsize=14)
plt.ylabel("Position (X)", fontsize=14)
plt.title(f"{npaths} Simulated Brownian Motion Paths with sdeint", fontsize=16)
plt.show()
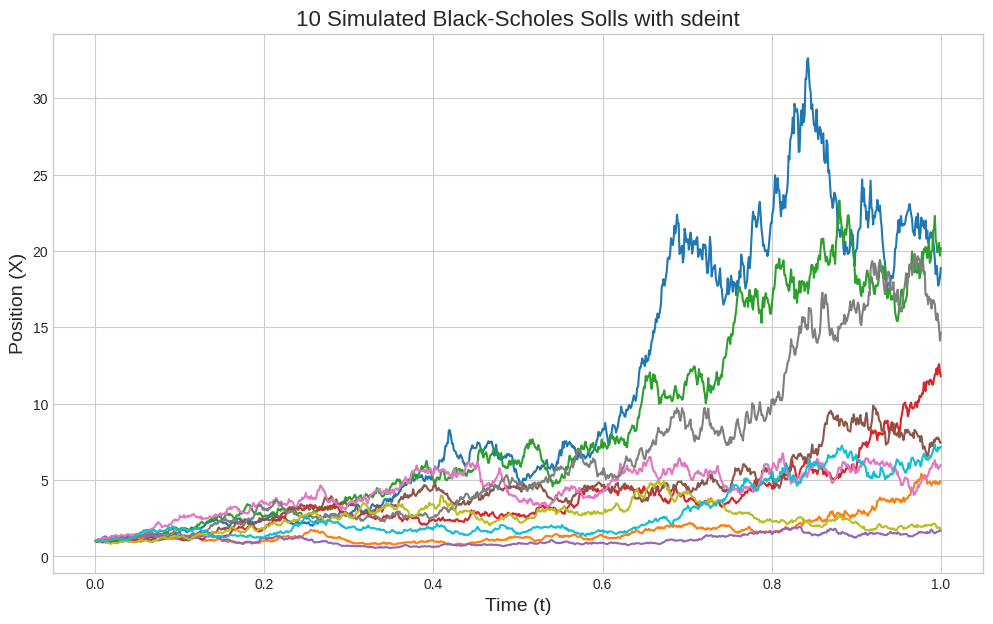
Di seguito si risolve invece l'equazione di Black-Scholes.
def f(x, t):
"""Drift function (zero for Brownian motion)."""
return λ*x
def g(x, t):
"""Diffusion function (constant for standard Brownian motion)."""
return μ*x
λ=2; μ=1
# Set Simulation Parameters
tspan = np.linspace(0.0, 1.0, 1001) # Time vector
x0 = 1.0 # Initial value
npaths = 10 # Number of paths to simulate
# Run the Simulation in a Loop and Plot
plt.style.use('seaborn-v0_8-whitegrid')
plt.figure(figsize=(12, 7))
# Loop to generate and plot each path
for i in range(npaths):
# The correct function is sdeint.itoint
result = sdeint.itoint(f, g, x0, tspan)
plt.plot(tspan, result)
# Add Labels and Title
plt.xlabel("Time (t)", fontsize=14)
plt.ylabel("Position (X)", fontsize=14)
plt.title(f"{npaths} Simulated Black-Scholes Solls with sdeint", fontsize=16)
plt.show()
Possiamo anche utilizzare un analogo metodo .stratint() per risolvere SDE che vengono formalmente rappresentate come \[dX(t) = f(X(t))dt + g(X(t))\circ dW(t),\quad X(0)= X_0,\quad 0 < t < T.\]
- sde: a simple tool for numerical stochastic differential equations, by Yuqiu Yang
- torchSDE, by Patrick Kidger
- Numerical Solvers for Stochastic Differential Equations, by Chaoming Wang