I concetti di convergenza forte e debole riguardano l'accuratezza di un metodo numerico su un intervallo finito $[0, T]$ per piccoli passi $\Delta t$.
Tuttavia, in molte applicazioni interessa il comportamento a lungo termine, $T\to\infty$, di un'equazione differenziale.
I limiti di convergenza della forma $\mathbb E|X_n - X(\tau_n)|< C\Delta t^\gamma$ o $|\mathbb Ep(X_n) - \mathbb Ep(X(\tau))| \le C\Delta t^\gamma$ non sono rilevanti in questo contesto poiché, generalmente, la costante $C$ cresce illimitatamente con $T$.
Per i metodi di equazioni differenziali ordinarie deterministiche è stata sviluppata un'ampia teoria della stabilità che fornisce informazioni sul comportamento dei metodi numerici nel limite $T\to\infty$ e $\Delta t$ fisso. Tipicamente, un metodo numerico viene applicato a una classe di problemi con una caratteristica qualitativa e viene analizzata la capacità del metodo di riprodurre tale caratteristica. Sebbene sia stata analizzata un'ampia varietà di classi di problemi, la più semplice, e forse la più rivelatrice, è l'equazione test lineare $\frac{dX}{dt} = \lambda X$, dove $\lambda \in C$ è un parametro costante. Per le EDS, è possibile sviluppare un'analoga teoria della stabilità lineare, come ora indichiamo.

Torniamo all'SDE lineare \[dX(t) = \lambda X(t)dt + \mu X(t)dW(t),\quad X(0) = X_0,\] con i parametri $\lambda$ e $\mu$ che possono essere complessi.
Nel caso in cui $\mu = 0$ e $X_0$ è costante, l'equazione si riduce all'equazione test lineare deterministica, che ha soluzioni della forma $X_0e^{\lambda t}$.
Se usiamo il termine stabile per indicare che $\displaystyle \lim_{t\to\infty}X(t)= 0$ per qualsiasi $X_0$, allora vediamo che la stabilità è caratterizzata da $Re\lambda < 0$.
Per generalizzare questa idea al caso delle SDE, dobbiamo essere più precisi su cosa intendiamo per $\displaystyle \lim_{t\to\infty}X(t)= 0$. Le variabili casuali sono oggetti di dimensione infinita e quindi le norme non sono equivalenti in generale. Considereremo le due misure di stabilità più comuni: media quadratica e asintotica. Supponendo che $X_0\not= 0$ con probabilità 1, le soluzioni della SDE lineare soddisfano \[\displaystyle \lim_{t\to\infty}\mathbb E X^2(t)= 0\iff Re\lambda +\frac{1}{2}|\mu|^2 < 0\] e \[\displaystyle \lim_{t\to\infty}|X(t)|= 0 \text{ con probabilità }1 \iff Re\left(\lambda -\frac{1}{2}\mu^2\right) < 0\] Il membro sinistro della prima condizione definisce cosa si intende per stabilità quadratica media, quello destro caratterizza completamente questa proprietà in termini dei parametri. Analogamente la seconda condizione definisce e caratterizza la stabilità asintotica. Ponendo $\mu = 0$, le caratterizzazioni collassano alla stessa condizione, $Re\lambda < 0$, che, ovviamente, si è verificata per la stabilità deterministica. Dalle due condizioni segue immediatamente che se l'SDE lineare è stabile quadratica media, allora è automaticamente stabile asintotica, ma non viceversa.
Quindi, in questo problema di test, la stabilità quadratica media è un requisito più stringente rispetto alla stabilità asintotica. Entrambe le definizioni di stabilità sono utili nella pratica.

Supponiamo ora che i parametri $\lambda$ e $\mu$ siano scelti in modo che l'equazione differenziale standard sia stabile in senso quadratico medio o asintotico. Una domanda naturale è quindi: "Per quale intervallo di $\Delta t$ la soluzione EM è stabile in senso analogo?". La versione quadratica media di questa domanda è facile da analizzare. Semplici proprietà del valore atteso mostrano che \[\displaystyle \lim_{i\to\infty}\mathbb E X^2_i= 0\iff |1+\lambda\Delta t|^2 +|\mu|^2\Delta t < 1\] La versione asintotica della domanda può essere studiata tramite la legge forte dei grandi numeri e la legge del logaritmo iterato, che porta a \[\displaystyle \lim_{i\to\infty}|X_i|= 0 \text{ con probabilità }1 \iff \mathbb E\log\left|1+\lambda\Delta t +\mu\sqrt{\Delta t}N(0,1)\right| < 0\]

Testiamo la stabilità della media quadratica per l'SDE con $X_0 = 1$ (costante) su $[0, 20]$ per due parametri che soddisfano la condizione e quindi il problema è stabile in media quadratica. Applichiamo EM su 50.000 cammini browniani discreti per tre diverse dimensioni di passo tra cui solo il terzo di questi, $\Delta t = \frac{1}{4}$, soddisfa il membro destro della condizione.

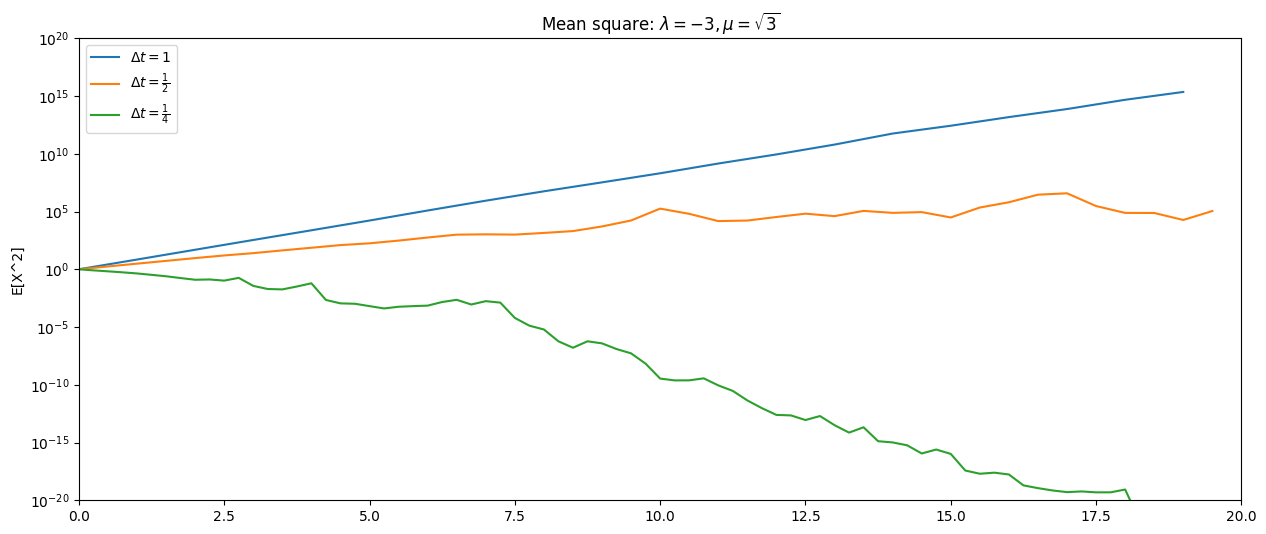
L'immagine traccia la media campionaria di $X_i^2$ in funzione di $t_i$. Si noti che l'asse verticale è scalato logaritmicamente. In questa immagine solo la curva per $\Delta t = \frac{1}{4}$ decade verso zero e, pertanto, questo test implica correttamente che solo per questo caso EM è stabile in media quadratica. Tuttavia, il numero di campioni utilizzati (50.000) non è sufficiente a risolvere completamente il comportamento; le tre curve dovrebbero essere linee rette. Ciò evidenzia il fatto che un campionamento semplicistico senza ulteriori controlli può portare a conclusioni fuorvianti.

Per esaminare la stabilità asintotica, utilizziamo parametri per cui l'equazione differenziale è asintoticamente stabile ( ma non stabile in media quadratica). Poiché la stabilità asintotica riguarda un evento di probabilità 1, applichiamo l'equazione quadratica media su un singolo cammino browniano discreto per alcuni valori di $\Delta t$, e poiché calcolare con un singolo cammino è economico, integriamo su $[0, 500]$. Si può dimostrare che solo il più piccolo di questi intervalli temporali soddisfa la condizione.

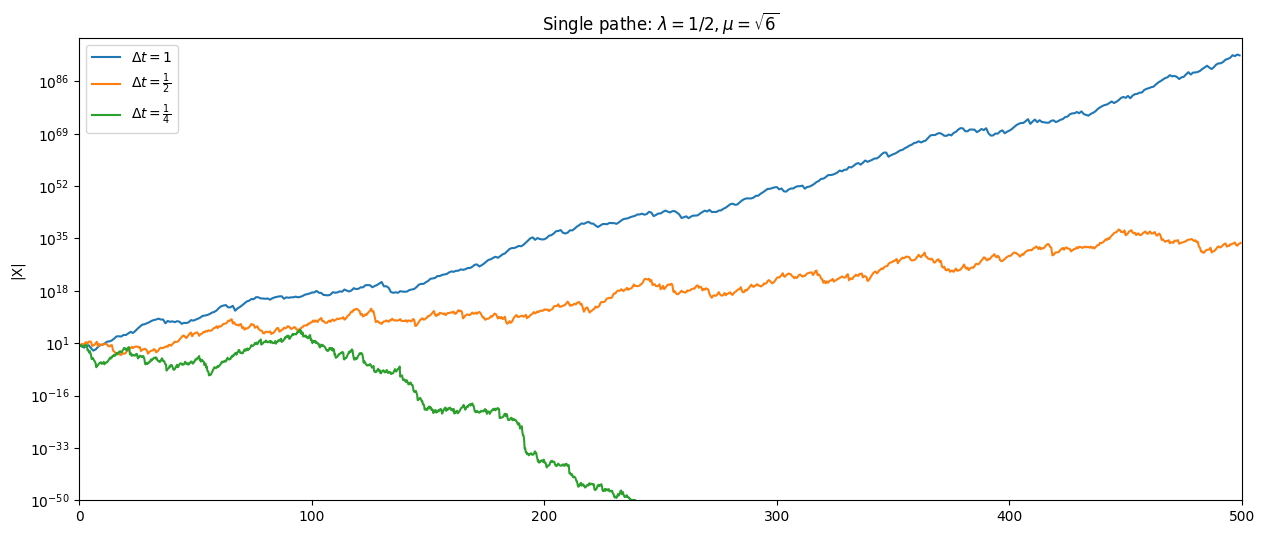
L'immagine mostra i grafici di $|X_i|$ in funzione di $t_i$ lungo il cammino. Osserviamo che solo la soluzione per $\Delta t = \frac{1}{4}$ sembra decadere a zero, in accordo con la teoria.