Accenniamo brevemente a un'altra differenza fondamentale tra calcolo stocastico e deterministico. Nel caso deterministico, se $\frac{dX}{dt} = f(X)$, allora, per qualsiasi funzione liscia $V$, la regola della catena, cioè della derivata di funzione di funzione, afferma che \[\frac{dV(X(t))}{dt} = \frac{dV(X(t))}{dX} \frac{dX(t)}{dt} = \frac{dV(X(t))}{dX}f(X(t))\] Supponiamo ora che $X$ soddisfi l'equazione differenziale standard di Itô $$dX(t) = f(X(t))dt + g(X(t))dW(t).$$ Qual è l'equazione differenziale standard analoga alla precedente per $V(X)$? Un'ipotesi ragionevole è $dV = \frac{dV}{dX}dX$, quindi \[dV(X(t)) = \frac{dV(X(t))}{dX}\left(f(X(t))dt + g(X(t))dW(t)\right) \] Tuttavia, un'analisi rigorosa che utilizza il risultato di Itô rivela che emerge un termine aggiuntivo e la formulazione corretta è \[dV(X(t)) = \frac{dV(X(t))}{dX}dX(t)+\frac{1}{2}g^2(X(t))\frac{d^2V(X(t))}{dX^2}dt\] che diventa \[dV(X(t)) = \left(f(X(t))\frac{dV(X(t))}{dX}+\frac{1}{2}g^2(X(t))\frac{d^2V(X(t))}{dX^2}\right)dt+g(X(t))\frac{dV(X(t))}{dX}dW(t)\] Anziché tentare di giustificare o addirittura di dimostrare, eseguiremo un esperimento numerico.
Consideriamo la SDE del processo di Cox-Ingersoll-Ross (CIR), un processo di radice quadrata con ritorno alla media che modella i prezzi delle attività.
\[dX(t) = (\alpha- X(t))dt + \beta \sqrt{X(t)}dW(t), X(0) = X_0,\]
con i parametri $\alpha$, tasso di mean-reversion (livello di lungo periodo), e $\beta$, volatilità (intensità del rumore), che sono costanti positive.
Si può dimostrare che se $X(0) > 0$ con probabilità 1, allora questa positività viene mantenuta per ogni $t > 0$.
Prendendo $V(X) = \sqrt X$ e applicando la precedente relazione si ha
\[dV(t) = \left(\frac{4\alpha-\beta^2}{8V(t)}-\frac{1}{2}V(t)\right)dt+\frac{1}{2}\beta dW(t)\]
α=2; β=1; T=1; N=200; δt=float(T)/N
Xo_1=1; Xo_2=np.sqrt(Xo_1)
Xem1 = np.zeros(N); Xem2 = np.zeros(N)
Xt_1=Xo_1; Xt_2=Xo_2
Xem1[0]=Xt_1; Xem2[0]=Xt_2
Δt = δt
for j in range(1,int(N)):
ΔW = np.sqrt(δt)*np.random.randn(1)
Xt_1 += (α-Xt_1)*Δt + β*np.sqrt(np.abs(Xt_1))*ΔW
Xem1[j] = Xt_1
Xt_2 += ((4.0*α-β**2)/(8*Xt_2) - Xt_2/2.0)*Δt + β/2.0*ΔW
Xem2[j] = Xt_2
ax=plt.subplot(111)
ax.plot(np.arange(0,T,Δt),np.sqrt(Xem1),'b-', np.arange(0,T,Δt),Xem2,'ro' )
ax.legend(("Direct solution", "Solution via chain rule"),loc=2)
plt.xlabel("t",fontsize=12)
plt.ylabel("V(X)",fontsize=12,rotation=0)
print( "Max disrepancy is: ", np.max(np.abs(np.sqrt(Xem1)-Xem2)))
plt.show()
Max disrepancy is: 0.01076564423988513
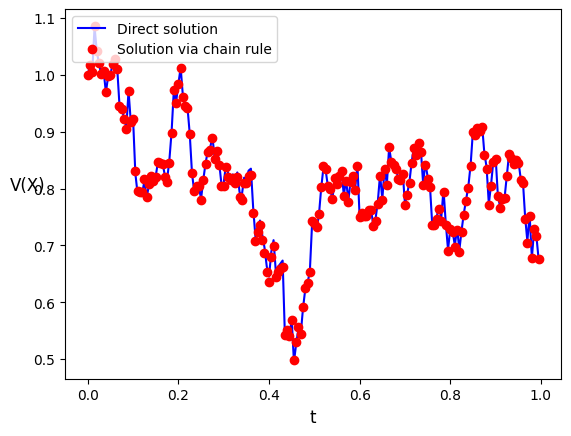
L'immagine mostra un buon accordo tra le due soluzioni, confermato da un controllo sulla discrepanza massima.