Abbiamo visto che EM ha ordine di convergenza forte $\gamma = \frac{1}{2}$, mentre il sottostante metodo deterministico di Eulero converge con ordine classico 1. È possibile elevare l'ordine forte di
EM a 1 aggiungendo una correzione all'incremento stocastico, ottenendo in tal modo il metodo di Milstein.
La correzione sorge perché lo sviluppo di Taylor tradizionale deve essere modificato nel
caso del calcolo Itô. Un cosiddetto sviluppo di Itô-Taylor può essere formato applicando il risultato di Itô
che è uno strumento fondamentale del calcolo stocastico. Per l'equazione differenziale differenziale stocastica
\[dX(t) = f(X(t))dt + g(X(t))dW(t),\quad X(0)= X_0,\quad 0 < t < T,\]
si ottiene il metodo di Milstein troncando lo sviluppo di Itô-Taylor in modo appropriato
\[ X_i = X_{i-1} + f(X_{i-1})\Delta t + g(X_{i-1}) (W(\tau_i) - W(\tau_{i-1}))+\]
\[+\frac{1}{2}g'(X_{i-1}) \left((W(\tau_i) - W(\tau_{i-1}))^2-\Delta t\right) ,\quad i = 1,2,\dots,L.\]
Applichiamo il metodo di Milstein all'equazione differenziale stocastica
\[dX(t) = rX(t)(K- X(t))dt + \beta X(t)dW(t),\quad X(0) = X_0,\]
che si verifica nella dinamica delle popolazioni. Qui, $r, K$ e $\beta$ sono costanti.
Prendiamo
$r = 2, K = 1, \beta = 0,25$ e $X_0 = 0,5$ (costante) e utilizziamo cammini browniani discretizzati
su $[0,1]$ con $\delta t = 2^{-11}$. La soluzione può essere scritta come un'espressione in forma chiusa che coinvolge un integrale stocastico. Per semplicità, consideriamo la soluzione di Milstein
con $\Delta t = \delta t$ come buona approssimazione della soluzione esatta e la confrontiamo con
l'approssimazione di Milstein utilizzando $\Delta t = 128\delta t, \Delta t = 64\delta t, \Delta t = 32\delta t$ e $\Delta t = 16\delta t$ su 500 percorsi campione.
Anziché utilizzare un ciclo for per variare i percorsi campione, eseguiamo il calcolo con tutti i percorsi simultaneamente.
r=2; K=1; β=0.25; Xo=0.5
T=1; N=2**11; δt=float(T)/N
M=500
R = [1, 16, 32, 64, 128]
# dW[s,i] è il i-esimo incremento per il s-esimo percorso
dW = np.sqrt(δt)*np.random.randn(M,N)
Xmil = np.zeros((M,5))
for p in range(5):
Δt = R[p]*δt # passi temporali
L = float(N)/R[p]
Xt = Xo*np.ones(M)
for i in range(1,int(L)+1):
# somma per ogni riga di dW dalla colonna R(p)∗(i−1) fino a R(p)∗i-1.
ΔW=np.sum(dW[:,range(R[p]*(i-1),R[p]*i)],axis=1)
Xt += r*Xt*(K-Xt)*Δt + β*Xt*ΔW + 0.5*β**2*Xt*(np.power(ΔW,2)-Δt)
Xmil[:,p] = Xt
Xerr = np.abs(Xmil[:,range(1,5)] - np.tile(Xmil[:,0],[4,1]).T)
Δtvals = np.multiply(δt,R[1:5])
plt.loglog(Δtvals,np.mean(Xerr,0),'b*-')
plt.loglog(Δtvals,Δtvals,'r--')
plt.axis([1e-3, 1e-1, 1e-4, 1])
plt.xlabel(r'$\Delta t$')
plt.ylabel(r'Sample average of $|X(T)-X_L|$')
plt.title('Milstrong',fontsize=16)
#### Least squares fit of error = C * Δt^γ ####
A = np.column_stack((np.ones((4,1)), np.log(Δtvals)))
rhs=np.log(np.mean(Xerr,0))
sol = np.linalg.lstsq(A,rhs)[0]
resid=np.linalg.norm(np.dot(A,sol) - rhs)
print('γ = ', sol[1],'residual = ', resid)
plt.show()
γ = 1.0076086343354078 residual = 0.018956612595115198
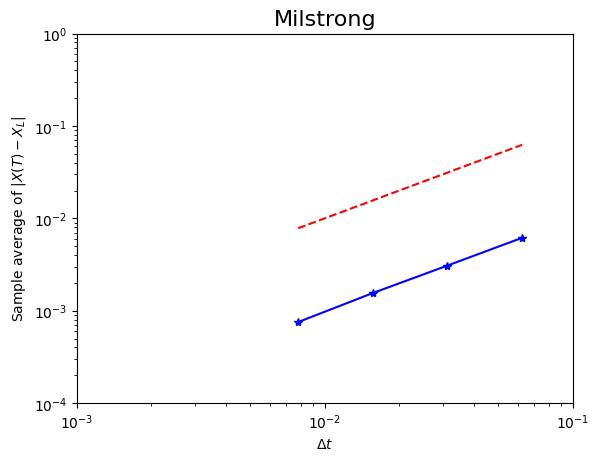
La figura mostra il grafico dell'errore logaritmo-logaritmo risultante insieme a una retta di riferimento con pendenza 1. L'adattamento con la legge di potenza dei minimi quadrati dà un valore per $\gamma$ e uno per il residuo.