Sport

Biliardo
Nel film d’animazione della W. Disney, "Paperino nel paese della matemagica", ( …16 min)BILLIARDS: An Introduction to Chaos Theory
da Serendip
Rimbalzi su biliardi di forma diversa
Dynamical billiards
From Wikipedia, the free encyclopedia
Rimbalzi su biliardi di forma diversa
It is known that in polygonal billiard always there is periodical trajectory. Make a regular hexagon, some convex polygon and some non-convex and try to find periodical paths!«per quanto sia bravo il portiere esiste sempre un’area della porta che non è comunque
raggiungibile dal centro. Si tratta degli estremi laterali, soprattutto le fasce in alto, che
equivalgono a circa 1/3 della superficie totale della porta». Per definire questo spazio sono
stati analizzati i tuffi di vari portieri di alto livello e si è calcolato geometricamente
l’inviluppo - così viene denominato - della parata. A dimostrazione di queste affermazioni
Bray cita i rigori di alcune celebri partite, analizzando il punto in cui la palla entra nella
porta. E si vede benissimo che tutti i tiri imparabili vanno sempre ai lati. «In pratica -
conclude Bray - vince chi ha i giocatori che sanno tirare nel modo più preciso. Le capacità
del portiere sono molto meno importanti».
Ken Bray
A volte arrendersi è razionale
by Killipop

Pallone o sfera?
in La scienza nel pallone di Nicola Ludwig e Gianbruno Guerrerio
Blast it like Beckham? Penalty tactics in soccer
di John Haigh
Quando tira un rigore, un giocatore di calcio si prefigge quale scopo, ovviamente, di segnare un goal. Egli può fallire in due modi: mancando del tutto lo specchio della porta oppure facendosi parare il tiro dal portiere!
Possiamo, quindi, considerare l'attività di tirare i rigori come un vero e proprio gioco a se stante, nel quale tanto il rigorista S quanto il portiere G possono scegliere in un insieme finito di tattiche.
Generalized Baseball Curves: Three Symmetries and You're In!
by Dean Allison, Ricardo Diaz, and Nathaniel Miller
Cucitura su una pallina da tennis, di Simona Riva
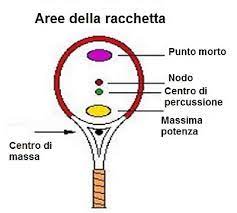
Cosa accade all’impatto
Blog di tuttoracchette
La matematica del tennis: così il sistema di punti favorisce chi perde
di Marta Russo su Wired.it
Secondo un nuovo modello, creato da un team di matematici dell'Università di Cambridge, il sistema di punteggio del tennis aumenta le probabilità che l'avversario sfavorito possa vincere, rendendo così il gioco ancora più eccitante.
Outer space: Ping-Pong is coming home
di John D. Barrow
Sulla cresta dell’onda
di Matteo Bartocci
Un matematico italiano in Coppa America
Intervista a Alfio Quarteroni
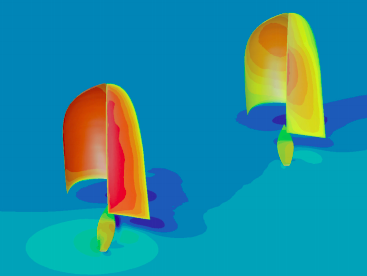
Simulazione numerica per la Coppa America di vela
di Nicola Parolini e Alfio Quarteroni
Mathematics in the Wind
di D. Detomi, N. Parolini e A. Quarteroni
Intervista della riviste Galileo e Pristem ad Alfio Quarteroni
La matematica della bicicletta
di D. Ambrosi, A. Bacciotti, G. RopoloNo Math= No Bicycling (How Math is Related to Bicycling)
By Daniel FerioliScience of Cycling
© ExploratoriumBicycle Math
by Timothy E. GoldbergMath in Motion The Bicycle
by Jason Achilich GED
Ciclismo e aerodinamica, il contributo della Galleria del Vento
Aerodinamica nel ciclismo: - Analisi e Calcolo
A cura di Marco Panzeri, Senior CFD Engineer, ANSYS ItaliaCiclismo e Aerodinamica
Prevedere una prestazione a cronometro, di Stefano SerniEnrico Perano
Il metodo scientifico applicato allo style slalom nel pattinaggio.Maths and Sport
These videos are of a series of lectures for the general public on 'The Mathematics of Sport' by Professor John D Barrow FRS, given for Gresham College.
This 'Maths and Sport' website, originally developed to celebrate the London 2012 Olympic and Paralympic Games, is part of the award-winning Millennium Mathematics Project at the University of Cambridge.
We created free online mathematical resources exploring maths and science through sport, and particularly through the Olympic and Paralympic Games. Resources include activities designed to develop problem-solving and mathematical reasoning skills for students aged 5 to 18 (UK Key Stages 1 to 5) and articles aimed at older students and the interested general reader.
We also developed a small collection of activities on Maths and Football in collaboration with Arsenal in the Community.
You can find all our articles and activities, arranged by Key Stage, using the tabs at the top of the page, or view content by sport or topic.