Vita

”... coloro che conoscono e comprendono i principi della matematica sembrano avere un sesto senso per le cose biologiche.”
Charles Darwin Lettere (1825-1859)
La dinamica dell’amore, da Laura e Petrarca a Jules e Jim
di Federico Peiretti su PolymathLa dinamica dell’amore
Modellistica matematica per le applicazioni 2015-16, UniFiLove Affairs and Differential Equations
di Steven H. StrogatzDifferential Equations of Love and Love of Differential Equations
di Isaac ElishakofIl valore delle leggi statistiche nella fisica e nelle scienze sociali
di Ettore MaioranaIl metodo entropico nelle applicazioni della meccanica statistica alle scienze sociali
tesi di laurea di Ilaria BrunettiTemporary bluffing, ..., is a very effective, though not unique, way for performing the switch.
Negli anni ’20 un matematico, Vito Volterra, e Alfred Lotka, supervisore in una compagnia di assicurazioni con numerosi interessi scientifici, posero le basi dell’ecologia teorica studiando ad esempio i cicli preda-predatore; nello stesso periodo, Ronald Fisher, fondatore della moderna statistica matematica, contribuì a formulare in modo matematico la teoria Darwiniana dell’evoluzione e a fondare la ”teoria genetica di popolazioni”.
Dagli anni ’70 il forte aumento di interesse per i modelli matematici in vari settori della biologia ha prodotto la “biologia matematica” o "biomatematica".
Dinamiche di popolazione
di S.Marsili-libelliPredatore-preda
Consider the Lotka-Voterra equations of interacting predator and prey systems
x'=x(a-cx-dy)
y'=-y(b-ex)-h
where all of x, y, a, b, c, d, k, n are positive, and
x represents the number of prey
y represents the number of predators
a is the growth rate of the prey.
b is the death rate of the predators independent of the prey.
d is the is the rate of consumption of the prey per predator.
a / c is the carrying capacity of the prey independent of the predators.
e is the growth rate of the predator per prey consumed,
h is prey harvesting.
This equations include the effect of limited resources on the food supply of the prey, and how the prey are culled or harvested. The following simulation demonstrates the solutions to these equations for a=1, b=0.25, c=0.01, d=0.02 and e=0.02.
Change the initial conditions and the harvesting to analyse the behaviour of the populations.
Modelli matematici dell’evoluzione biologica
di Carlotta MaffeiLauree Magistrali in Biologia e Tecnologie Cellulari e Ecobiologia, Dipartimento di Matematica de La Sapienza Universitá di Roma
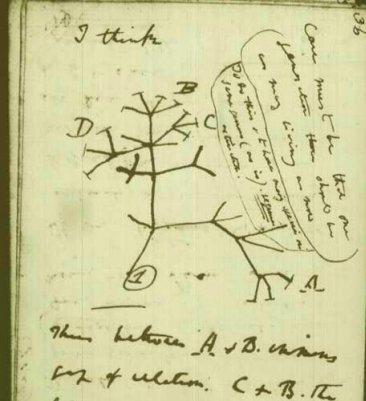
Uno dei modi in cui la scienza ha realizzato l’aspirazione umana di prevedere il futuro non proviene dallo studio degli astri o dalla interpretazione delle carte o dei sogni, ma, di nuovo, dalla codifica degli eventi in formule e numeri. In altre parole, uno dei codici che la scienza ha utilizzato, sin dall’antichita’, per descrivere aspetti del mondo esterno in modo da poter trarre previsioni dalla descrizione stessa, è quello della traduzione dei fenomeni in termini matematici. Il vantaggio che presenta un approccio di questo tipo è stato riconosciuto nel fatto che, una volta attuata questa trascrizione, la questione concreta in studio si trasforma in un problema matematico che si affronta, ovviamente, utilizzando l’apparato e le regole della matematica. L’eventuale corretta soluzione del problema matematico permette di trarre alcune conseguenze o previsioni teoriche. Se si riconosce, tramite l’analisi sperimentale, che le previsioni sono corrette, la formulazione matematica del fenomeno viene accettata come modello matematico; in caso contrario, si modifica la trascrizione di cui sabbiamo parlato e si ripete il procedimento, fino ad ottenere una accettabile precisione nella descrizione delle conseguenze.
Matematica ed Ecologia: un’interazione feconda
di Marino Gatto su Bollettino dell'Unione Matematica Italiana Serie 8, vol. 5-A (2002) — La Matematica nella Società e nella CulturaVirus
Da Wikipedia, l'enciclopedia libera.
Coronavirus
DNA
Da Wikipedia, l'enciclopedia libera.Sequenziazione del genoma
Da Wikipedia, l'enciclopedia libera.
Vita artificiale
Da Wikipedia, l'enciclopedia libera.The Blind Watchmaker: Why the Evidence of Evolution Reveals a Universe Without Design
è il libro di Richard Dawkins, nel quale egli presenta una spiegazione, e una discussione, della teoria dell'evoluzione mediante la selezione naturale e inventa i biomorfi, piccole "creature" disegnate con 9 semplici "geni" interi.Biomorfi
Morphs are artificial creatures, but like natural ones, they have a genome (you know, a set chromosomes). What you see is the phenotype, but the code is the genome. Morphs are little beings, so they have only one little chromosome, composed of only nine genes. These genes are represented by letters. It can be any combination taken from A to M, except the last which can have only the value from I to N. Therefore, there are 4,894,384,326 types of different morphs you can display!


