Natura

“Lo scienziato non è l'uomo che fornisce le vere risposte; è quello che pone le vere domande.”
Claude Lévi-Strauss
“Per quelli che non conoscono la matematica è difficile arrivare al vero apprezzamento della bellezza, la grandissima bellezza della natura. [...] Se volete conoscere e apprezzare la natura è necessario capire la lingua che parla.”
La legge fisica, Richard Philips Feynman (1918-1988)
Albrecht Dürer
Studia una sorta di “geometria del corpo umano ” che lo porta a costruire un “reticolo uniforme ”, cioè un piano quadrettato, all’interno del quale le fattezze umane hanno una griglia di riferimento, la stessa idea che portò il grande naturalista scozzese D ’Arcy Wentworth Thompson ad una sorta di “studio matematico delle specie della natura ”…
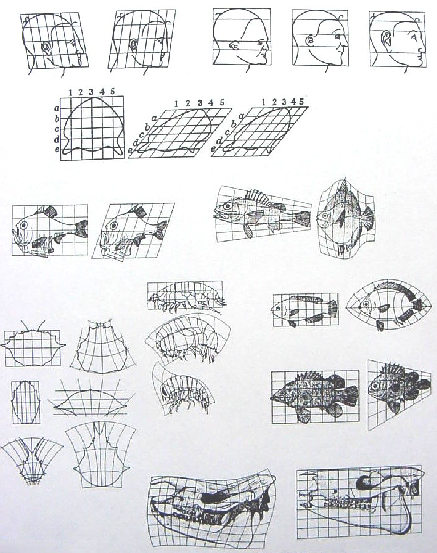
On Growth and Form, 1917
Wentworth Thompson D'Arcy (1860-1948)
Le onde del mare, le linee della salsedine sulla battigia, la fugace curva della baia sabbiosa tra i promontori, il profilo dei colli, la forma delle nuvole, sono tanti enigmi di forma, sono tanti problemi di morfologia.
Using a computer to visualise change in biological organisms
The True Geometry of Nature
[Seeing through Mathematics]Dalle forme naturali ai modelli
A cura dei docenti dell'ISA Sperimentale di Monza
Superformula Johan Gielis
Da Wikipedia, l'enciclopedia libera.
In questa descrizione molti ritroveranno il proprio piacere di allineare oggetti dalla forma interessante, piccoli appunti visivi di cui tenere conto, per chissà quali percorsi futuri. Chi si occupa di progettazione conosce l'importanza dell'educazione silenziosa che queste forme ci offrono. Il percorso didattico di cui tratteremo si propone, in qualche modo, come una riflessione su questi temi. È un viaggio guidato nel mondo della forma delle conchiglie, condotto all'interno della didattica di una scuola di design. La finalità primaria di questo lavoro è quella di proporre agli studenti metodi di lettura a carattere prevalentemente scientifico.
Bolle di sapone
Frattali
di Eliana Argenti e Tommaso BientinesiNel 1960 espresse in una famosa conferenza l'intento di capire perché le leggi della fisica si possono descrivere così facilmente con le regole della matematica. Senza queste regole molti fenomeni dell'universo sarebbero infatti incomprensibili. Ma se è pura e astratta come dicono, per quale straordinaria coincidenza la matematica è in grado di rappresentare gli oggetti così concreti e mutabili del mondo fisico? In base a quale strano fenomeno uno strumento tanto astratto ci permette di comprendere il mondo reale? È solo un caso o esiste un'entità ancora sconosciuta che ha ordito questo complotto dei numeri?
Per David Deutsch il presunto complotto è solo una conseguenza della natura della matematica che, «lungi dall'essere qualcosa di puro e astratto, è un processo fisico». In altre parole, se il mondo in cui viviamo è comprensibile lo dobbiamo in buona parte al caso
L'irragionevole efficacia della matematica
di R. W. Hamming, 1980