Matematica nella musica

«la musica è una disciplina in cui si parla di numeri»
Cassiodoro (vi sec.)
«[la musica è] emanazione sensibile di strutture matematiche»
Agostino
«Non è la ragion prossima ed immediata delle forme de gl’intervalli musici la lunghezza delle corde, non la tensione, non la grossezza, ma sì bene la proporzione de i numeri delle vibrazioni e percosse dell’onde dell’aria che vanno a ferire il timpano del nostro orecchio, il quale esso ancora sotto le medesime misure di tempi vien fatto tremare»
Galileo, nei Discorsi e dimostrazioni matematiche intorno a due nuove scienze (1638).
Matematica scienza musicale
di Maurizio AgròSecondo la tradizione, la nascita della scienza musicale risalirebbe a Pitagora, che scoprì, percuotendo un’anfora piena d’acqua a cui via via ne andava aggiungendo dell’altra, che si generava la stessa nota ma più acuta. Una variante dell’aneddoto è tramandata da Giamblico di Calcide (iii sec. d.C.): l’intuizione di Pitagora sarebbe merito di un fabbro crotonese che martellava il ferro con mazze di diversa grandezza. Tra i rumori così emessi, alcuni risultavano più gradevoli di altri. Pitagora li chiamò suoni consonanti e scoprì che erano dovuti a martelli i cui pesi stavano in precisi rapporti.
Matematica e… l'armonia del mondo
di Armando Bertinetti - Liceo Volta di Torino, Alessandra Del Piccolo - I.I.S. Europa Unita di Chivasso, su PolymathPitagora disse: "Tutto è numero"; Keplero e la "musica delle sfere"; Newton e i pitagorici.
La concezione fisico-matematica della musica della scuola pitagorica si salda, nell’Europa medievale, con la tradizione del pensiero cristiano. Con la celebre definizione Musica est scientia bene modulandi Agostino trasmise l’idea che la musica fosse una scienza delle proporzioni numeriche. Il trattato più noto della scienza musicale fu però il De institutione musica di Boezio, nel quale, a partire dagli esempi dei teorici greci della musica, veniva matematizzata la gamma dei suoni e veniva ribadito il fondamento teorico per il quale solo due suoni in successione di diversa altezza che potevano essere espressi attraverso rapporti matematici semplici potevano essere considerati consonanti, quindi gradevoli all’udito nella pratica esecutiva.
La natura scientifica dell’esperienza musicale così impostata costituì un assioma nel mondo medievale occidentale non solo per i teorici, ma anche per i cantori di musica sacra. Il canto ecclesiastico, infatti, subì nel corso del secolo IX un processo di unificazione e standardizzazione che coincise con l’organizzazione del repertorio chiamato “gregoriano” in sistemi scalari (modi) desunti dal trattato di Boezio. Non stupisce, quindi, che all’interno del sistema didattico medievale la musica, intesa ora come arte del canto della chiesa, continuasse a essere inserita nel quadrivium delle arti liberali al fianco di aritmetica, geometria e astronomia, anziché nel trivium in compagnia di grammatica, retorica e dialettica, le arti della parola su cui quel canto, in ultima istanza, era basato.
da Introduzione on line al pensiero e alle pratiche della musica Università di Siena
Compendium musicae
(1618) René DescartesÈ dell'opinione che una semplice analisi matematica della consonanza possa fornirci le nozioni fondamentali sul modo di produrre il suono e quindi sulla natura della musica. Per Cartesio ogni oggetto piacevole viene percepito come semplice, le serie armoniche sono più semplici delle serie geometriche e quindi da preferire. Egli traduce i rapporti musicali in segmenti di linea in modo da renderli visibili all'occhio e quindi intuitivamente più chiari.


Harmonices Mundi
(1619) di Johannes KeplerDiscute alcune analogie fra l'armonia musicale, la congruenza nelle forme geometriche e i fenomeni fisici. L'ultima parte del libro contiene l'enunciazione della terza legge di Keplero sul moto dei pianeti.
Harmonices Mundi
traduzione del Liceo Scientifico Benedetto Croce - PalermoPremio Archimede 2018 - “Matematica è Cultura”

«La terra canta Mi, Fa, Mi: potete dedurre persino dalle sillabe che in questo mondo non vi è che Miseria e Fame»

Harmonie universelle
contenant la théorie et la pratique de la musique, 1636Marin Mersenne (1588-1648)- premier livre de la Nature des Sons
- second livre des Mouvemens de toutes sortes de corps
- troisiesme livre des Mouvemens ... de chords ...
- traité Mechanique
- traité de la Voix e des Chants.
- livre second des Chants
- des Consonances, des Dissonances, des Genres, des Modes, de la Composition
- livre second des Dissonances
- livre troisieme des Genres, des Especies, des Modes, des Systemes e de la Musique
- livre quatriem de la Composition
- livres des Instrumens
- livre des Orgues
- livre des Instrumens de percussion
- livre de l'utilité de l'Harmonie
... il y a douze ou treize choses fort considerables: celle des six liures des Consonances, où l'on void sept choses à remarquer; celle du livre de la Voix, laquelle contient quatre ou cinq choses excellentes pour l'establissement du plus parfaict Idiome: celle des Instrumens, où l'on a tous les differens characteres, & leurs noms, dont on use dans les Imprimeries: & celle de l'Orgue dans laquelle sont suppleez beaucoup de choses appartenantes au livre de l'Orgue: & apres avoir corrigé toutes les fautes qui sont marquees à la fin desdites Prefaces, ou à la fin du troisieme livre des Mouvemens, du septiesme livre des Instrumens de Percussion, par lesquelles ie desire que l'on commence, à raison que celles des quatre premiers liures des Consonances y sont marquees, qui sont fort notables, à cause des notes & de la pratique, & celles qui sont à la fin du livre de l'utilité de l'harmonie, lequel on peut faire relier le premier: apres, dis-je, avoir fait tout cecy, l'on pourra lire les Propositions suivantes, afin de voir tout d'un coup ce qui est contenu dans tous les livres de cet oeuvre; quoy que l'explication ou la preuve de plusieurs Propositions contienne souvent beaucoup plus qu'elles ne promettent à leur lecture: de sorte qu'elles peuvent recompencer celles qui donnent moins que ce que l'on attend.
- I
- De sono et auditu.
- De suavitate et principiis harmoniae.
- De musica in genere.
- De consonantiis.
- De consonantiarum successione.
- II
- De seriebus consonantiarum.
- De variorum intervallorum receptis appellationibus.
- De generibus musicis.
- De genere diatonico-chromatico.
- III
- De aliis magis compositis generibus musicis.
- De consonantiis in genere diatonico-chromatico.
- De modis et systematibus in genere diatonico-chromatico.
- De ratione compositionis in dato modo et systemate dato.
- De modorum et systematum permutatione.
Il Tentamen novae theoriae musicae di Leonhard Euler
di Alvise De PieroPaperino nel paese della matemagica
della W. DisneyDopo aver ascoltato un uccello recitare le prime 15 cifre di pi greco, Paperino sente la voce dello "Spirito d'Avventura" che lo guiderà nel suo viaggio attraverso "il Paese delle Meraviglie della Matematica". Prendendo confidenza con lo spirito intuisce una possibile relazione tra i numeri e la musica e di colpo viene catapultato nell'antica Grecia dove Pitagora e i suoi compagni tengono una jam session con il papero. Lo spirito spiega che Pitagora realizzò rudimentali forme di musica che sono alla base di quella moderna, come il jazz, ancora di moda nell'America degli anni Cinquanta. Paperino stringe la mano a Pitagora, che svanisce subito lasciandogli sulla mano un simbolo, il pentagramma, che rappresenta la segreta società pitagorica.
Dal minuto 2.29
Musica e matematica
di Angelo Guerraggio su Enciclopedia della Matematica (2013) TreccaniMathematics and Music
di David Wright
Musica e Rivoluzione Scientifica
a cura di Redazione Torinoscienza - Anna Maria LombardiMusic + Math
Santa Fe InstituteIf math is pattern, and sound is vibration, music is sound shaped and patterned. Math can help us understand the rhythms, melodies, and harmonies that fascinate our brains and stir our hearts.
Matematica, geometria e musica
Alberto Conte, Moreno Andreatta con la partecipazione di Paolo Conte
Buone vibrazioni tra pentagramma, forme e formule
GiovedìScienza 15 DICEMBRE 2016
The Tonnetz
Ci si può così rendere conto di come il calcolo combinatorio sia nato dalla curiosità di un teorico della musica, quel padre Marin Mersenne che voleva calcolare tutte le melodie possibili partendo da una rappresentazione circolare delle note musicali, anticipando così di quasi un secolo il primo trattato di calcolo combinatorio e probabilistico. O ancora come la teoria dei grafi sia nata dall’idea del matematico Leonardo Eulero di caratterizzare i percorsi possibili che attraversano i vari ponti della città di Königsberg partendo da una rappresentazione geometrica bidimensionale degli accordi musicali, lo Speculum Musicae, che la musicologia contemporanea ha riscoperto e ribattezzato “reticolo di note” (o Tonnetz).
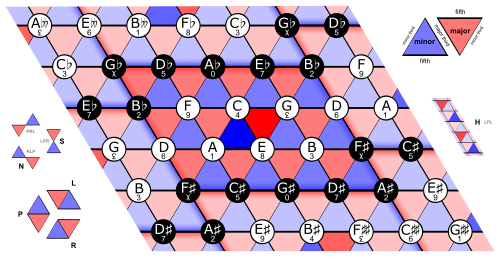
The Tonnetz su Wikipedia
Pianos and Continued Fractions
di Edward G. Dunne, American Mathematical Society
Musica e Matematica
rapporti concreti tra l'arte e la scienza più astratte, esplorati dai punti di vista delle due discipline intervento di Carlo Dapueto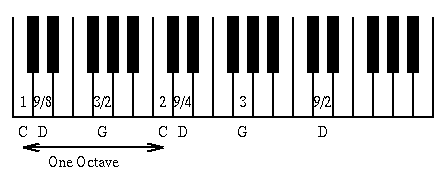
Lezione su musica e matematica
di Piergiorgio Odifreddi (Repubblica@Scuola)Math in Music
di Eugenia Cheng
In this fun explainer series, Dr. Eugenia Cheng shows everyone a way in, enhancing our understanding and enjoyment of both music and math
