Matematica e fisica del suono

...ed i suoni allora son fatti, e sentiti in noi, quando (senz'altre qualità sonore o transonore) un frequente tremor dell'aria, in minutissime onde increspata, muove certa cartilagine di certo timpano ch'è nel nostro orecchio.
Galileo
Nell'antichità
Pitagora (c. 550 a.c.) sapeva che il moto dell'aria prodotto da un corpo vibrante che suona una singola nota musicale è anch'esso vibratorio della stessa frequenza del corpo.
Erone di Alessandria (I sec. - III sec. d.c. circa) affermava che il suono è originato dalla propagazione di una compressione e di un impulso.
La possibilità che il suono fosse un fenomeno simile al propagarsi delle onde sull'acqua fu sostenuta ad esempio da Crisippo(c. 240 a.c.), dall'architetto e ingegnere romano Vetruvius (c. 25 a.c.), dal filosofo Boethius ( 480-524). Tale interpretazione era coerente con l'affermazione di Aristotele (384-322 a.c.) secondo cui il movimento dell'aria è causato da una sorgente che "spinge in avanti in tal modo l'aria vicina, in modo che il suono viaggia inalterato in qualità tanto lontano quanto il disturbo dell'aria consente di giungere."
Nel diciassettesimo secolo
L'acustica diventa scienza con lo sviluppo della meccanica e l'affermarsi del metodo sperimentale.
- Otto von Guericke (1602-1686) mostrò che l'aria è indispensabile per la propagazione del suono.
- Pierre Gassend (1592 - 1655) è spesso ricordato tra chi per primo effettuò misure della velocità del suono. Sosteneva che il suono fosse dovuto a sciami di "atomi" emessi dai corpi sonori, che la sua velocità fosse quella degli atomi e che la frequenza fosse il numero di atomi emessi per unità di tempo.
- Relazioni empiriche tra lunghezza delle corde vibranti e frequenza dei suoni furono determinate da Marin Mersenne (1588 - 1648) spesso indicato come "padre dell'acustica".
La descrizione di Mersenne, nell'opera Harmonic universelle (1636), della prima valutazione della più piccola frequenza udibile (a 84 Hz) evidenzia come avesse già compreso che il rapporto tra le frequenze di due corde vibranti relative a due noti musicali nell'intervallo di un'ottava è 1 : 2. L'armonia (consonanza) tra tali note è dunque legata al fatto che il rapporto tra le frequenze di oscillazione dell'aria è anche 1 : 2, coerentemente con l'ipotesi dell'equivalenza della frequenza del moto della sorgente e quello dell'aria. - Robert Boyle (1627-1691) mostrò nel 1662 che l'aria ha proprietà elastiche.
- Studi sistematici e dettagliati furono eseguiti da Joseph Sauveur (1653 - 1716) al quale è dovuto anche il termine "acustica". Sauveur spiegò la formazione delle onde stazionarie introducendo i i termini nodo e ventre di un'onda, il termine armoniche per i multipli interi delle frequenze. Descrisse il fenomeno dei battimenti. Determinò i limiti di udibilità.
- Esempio in Italia di studi sperimentali condotti con attenzione al metodo sono le Esperienze intorno ai movimenti del suono nei Saggi Naturali Esperienze di Lorenzo Magalotti nel 1667, dove in particolare si determina che il suono percorre 1 miglio (=1653 m) in 5 s.
- La teoria matematica della propagazione del suono inizia con Isaac Newton (1642-1727), che nei Principia (1686) inserisce una interpretazione del suono come impulsi di "pressione" trasmessi attraverso le particelle fluide confinanti. Attraverso diagrammi illustrava la divergenza dei fronti d'onda dopo il passaggio attraverso una fenditura.
Ricavò una formula per la velocità del suono.
L'analogia con le onde che si propagano nella superficie di separazione tra l'acqua e l'aria fu rafforzata dalla convinzione che il moto dell'aria associato con il suono è oscillatorio, dall'osservazione che il suono viaggia con velocità finita e, non ultimo, dal fatto noto che il suono come le onde sull'acqua aggira gli angoli (fenomeno della diffrazione).
In particolare per Galileo Galilei
- ...ed i suoni allora son fatti, e sentiti in noi, quando (senz'altre qualità sonore o transonore) un frequente tremor dell'aria, in minutissime onde increspata, muove certa cartilagine di certo timpano ch'è nel nostro orecchio.
- ... Toccata, la corda comincia e continua le sue vibrazioni per tutto 'l tempo che si sente durar la sua risonanza: queste vibrazioni fanno vibrare e tremare l'aria che gli è appresso, i cui tremori e increspamenti si distendono per grande spazio
- ... il suono si conduce al nostro udito in tempo men breve di quello che si conduca il lume
Nel diciottesimo secolo
In seguito allo sviluppo dell'analisi matematica venne affrontato uno studio sistematico dei fenomeni acustici, in particolare le soluzioni analitiche dei classici problemi delle corde vibranti, dei tubi sonori, delle lastre, delle membrane flessibili.
- Brook Taylor (1685-1731), celebre per aver mostrato come qualunque funzione è riconducibile a un polinomio (eventualmente di grado infinito), determinò, mediante il calcolo, le prime formule sul problema della corda vibrante.
- Daniel Bernoulli (1700 - 1782) studiò le vibrazioni trasversali delle verghe e sviluppò la teoria dei tubi d'organo.
- Di quest'ultima si occupò anche Lagrange (1736-1813) pubblicando i risultati nelle Memorie di Torino
- Leonhard Euler (1707 - 1783) studiò le verghe vibranti ed i tubi ad "ancia battente". Nel 1739, partendo dalla formula data da Taylor sui modi di vibrazioni di una corda, scrisse uno dei primi saggi di teoria scientifica della musica.
- Prime ipotesi sul fenomeno dei battimenti, già noto ai costruttori d'organo, che avviene in presenza di due suoni di frequenza poco diversa. Sauver (1653-1716) ne attribuì la causa alle concordanze fra le vibrazioni del primo suono e quelle del secondo per cui il suono udito dovuto ai battimenti ha frequenza pari alla differenza fra le frequenze dei due suoni.
Lagrange nella sua memoria sulla Natura e propagazione del suono precisò che se la differenza fra le frequenze è così grande da superare il limite dei suoni percettibili i battimenti non sono più percepiti dall'orecchio come suoni distinti ma si avvertono come un suono unico. Era il cosiddetto terzo suono che il violinista Tartini diceva si sarebbe prodotto in concomitanza di altri due suoni. Questo fenomeno fu sfruttato per la misura dell'altezza dei suoni per confronto con suoni campione: quando i battimenti hanno frequenza molto bassa i due suoni da confrontare sono circa della stessa altezza. - Pierre-Simon de Laplace (1749 - 1827) corresse la formula sulla velocità del suono (v/γ)²=p/δ, così in accordo con l'esperienza, introducendo correttamente i calori specifici adiabatici.
- Un metodo per la misura della velocità del suono nei gas e nei materiali venne invece trovato da Ernst Florens Friedrich Chladni (1756-1827) alla fine del secolo. A Chladni è anche dovuta la spiegazione dell'eco, la determinazione della soglia di udibilità fissata a 22000 vibrazioni al secondo, e studiò i modi di vibrazioni delle lamine elastiche visualizzando (figure dui Chladni) le linee nodali attraverso polvere che vi si raccoglie per assenza di vibrazione.
- L'equazione dell'onda è apparsa in una quantità di contesti, incluso la propagazione del suono in aria.
Nel diciannovesimo secolo
Le misure della velocità del suono nei mezzi si intensificarono nel XIX secolo.
- Studi sulla velocità del suono in liquidi e solidi sono associati ai nomi di Jean Baptist Biot (1774 - 1862), Daniel Colladon (1802 - 1893), Charles Sturm (1803 - 1855) e Jules Violle (1841 - 1923).
- Per misurare la velocità di propagazione del suono nell'acqua (alla temperatura 8,1°C), Colladon e Sturm, nel 1827 misurarono il tempo impiegato dal suono di una campana immersa del lago di Ginevra per percorrere 13,487 Km.
Simultaneamente alla percussione avveniva l'incendio di una certa quantità di polvere da sparo nello stesso punto dove si trovava la campana. Si misurava l'intervallo di tempo tra la visione della vampata e la percezione del suono ottenuta attraverso un ricevitore a forma di periscopio rovesciato. - Jean Baptiste Biot (1774-1862) misurò la velocità del suono nei metalli. Questa misura veniva ottenuta per differenza dei tempi di percezione dei due suoni che giungevano ad un osservatore lungo un tubo metallico contenente aria: il primo suono era quello trasmesso dal metallo stesso, il secondo trasmesso dall'aria e quindi propagato con velocità nota.
- L'acustica, come scienza, trova la sua sistemazione organica nel "A treatise on sound" di J.W.S. Reyleigh alla fine del secolo
Nel ventesimo secolo
Dall'inizio del 900, con lo sviluppo di strumenti elettrici ed elettronici, l'acustica sperimentale e le applicazioni tecnologiche hanno nuovo impulso. Si aprono possibilità nuove e nascono nuovi campi d'appplicazione: telecomunicazioni, produzione, registrazione e riproduzione dei suoni. Attualmente possiamo suddividere l'acustica in varie branche, sebbene in modo talvolta artificioso:
- acustica fisica: studio della generazione delle onde elastiche di qualsiasi natura, loro propagazione ed interazione con la materia (importante per lo studio geologico del sottosuolo);
- acustica fisiologica: studio della fonazione e dell'udito;
- psicoacustica: studio delle sensazioni uditive e loro conseguenze psicologiche (importante nel campo delle telecomunicazioni);
- ultracustica: studio delle proprietà e degli effetti degli ultrasuoni in campo biologico, medico ed industriale
- acustica applicata nei suoi vari aspetti: elettroacustica (HIFI, ecc.), acustica architettonica ed ambientale (sale da concerto, isolamento, inquinamento acustico, ecc.), acustica musicale (strumenti per la produzione dei suoni, sintetizzatori).
Museo di Fisica, Collezione acustica
La Sapienza, RomaFisica Onde Musica
Matematica e fisica del suono e della musica, UniMoRe.Physics of Music - Notes
di B. H. SuitsThe Soundry
an exciting, interactive, and educational web site about sound by Alex Kulesza, David Green, and Granite Christopher
Jean Baptiste Joseph Fourier
Un matematico freddoloso e l'effetto serra
di Elena Prestini
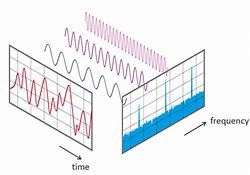
Tutti i fenomeni ciclici, le onde luminose, le maree oceaniche e i cicli solari sono scomponibili in un insieme di oscillazioni elementari, rappresentate da una sinusoide. In questo modo, si può sostituire a un’unica funzione – difficile però da trattarsi matematicamente – una serie più maneggevole di seni e coseni. La loro somma ricostruisce la funzione originaria.
Analisi di Fourier
in altre pagine di questo sito.