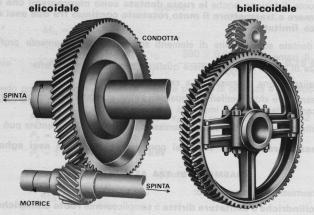
AI fine di ridurre gli inconvenienti che una trasmissione a ruote di frizione comporta (ad esempio slittamenti), nelle ruote dentate la trasmissione del moto potenza è affidata alle spinte che si trasmettono reciprocamente i denti che sporgono dalle corone delle ruote (Figura 1).
 |
Le ruote dentate per la trasmissione del moto tra assi paralleli possono essere:
-
cilindriche a dentatura diritta
-
cilindriche a dentatura elicoidale semplice
-
cilindriche a dentatura bielicoidale
-
cilindriche a dentatura cicloidale
|
|
|
|
Fig 2 |
Fig 3 |
Tutte queste a loro volta possono essere interne o esterne:
-
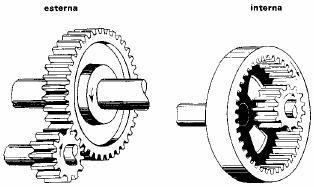
Fig. 4
Uniformità del movimento
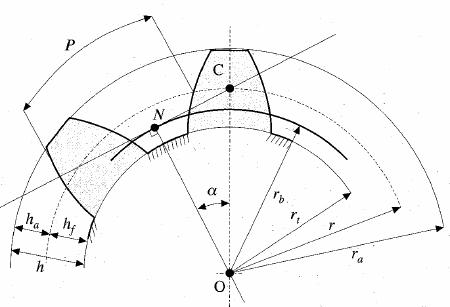
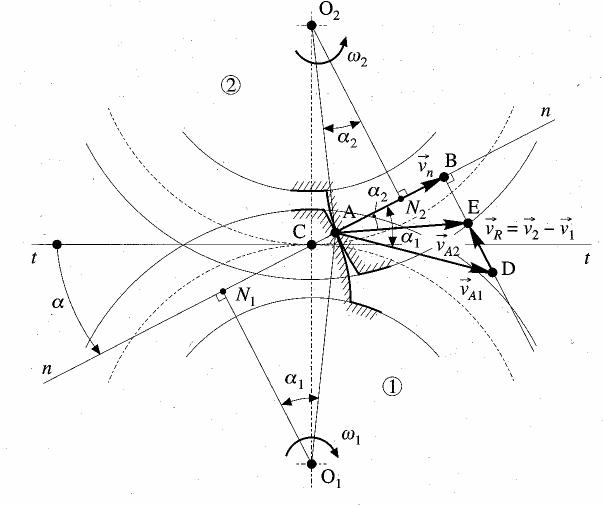
La trasmissione del moto deve in ogni caso svolgersi con la massima regolarità, idealmente senza urti, rispettando la costanza del rapporto di trasmissione. A tal proposito esaminiamo il moto di una coppia di ruote dentate cilindriche a denti diritti osservandone le condizioni di contatto fra i profili coniugati (Figura 1): ognuna delle due ruote dentate fa riferimento a una circonferenza particolare (circonferenza primitiva, come sarà in seguito specificato); siano le due circonferenze di centro rispettivamente O1 e O2, tangenti in C, e sia la coppia di denti in presa a contatto nel punto A. Considerato tale punto pensato appartenente prima alla ruota (1) motrice, poi alla ruota (2) condotta, le relative velocità periferiche istantanee risultano:
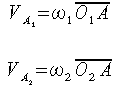
Al contatto i due
denti non devono urtarsi né distanziarsi, a tal proposito si conduca
da A la retta (n n) di contatto (o di pressione o ancora normale
di contatto) perpendicolare alla tangente del profilo di entrambi i denti
(deve essere comune, altrimenti o i denti si compenetrano o non si toccano)
nel punto di contatto A; inclinata di un angolo a
rispetto all'orizzontale (perpendicolare alla congiungente i centri O1
e O2). Dalla
figura 8.5 si osserva che, affinché non vi siano né urti,
né distanziamenti fra i profili, è necessario che le proiezioni
di ![]() ,
sulla retta (n n)
siano uguali, ovvero che la velocità relativa in direzione normale
alla superficie di contatto sia nulla. Anche in questo caso non è
comunque assicurata
l'assenza di strisciamenti relativi poiché esiste sempre, a eccezione
del punto notevole C, una velocità relativa tangenziale alle superficie
di contatto, causa di attriti e quindi di usura (la velocità
,
sulla retta (n n)
siano uguali, ovvero che la velocità relativa in direzione normale
alla superficie di contatto sia nulla. Anche in questo caso non è
comunque assicurata
l'assenza di strisciamenti relativi poiché esiste sempre, a eccezione
del punto notevole C, una velocità relativa tangenziale alle superficie
di contatto, causa di attriti e quindi di usura (la velocità ![]() in
figura 8.5).
in
figura 8.5).
Dall'esame della figura 8.5 si ricavano le condizioni di similitudine fra i triangoli:
![]()
(siano N1, ed N2 i piedi delle perpendicolari mandate dai centri delle ruote alla normale di contatto n n). Stabiliti gli angoli:
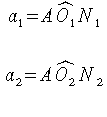
si ha pure:
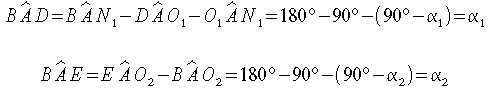
Ne segue che: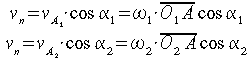 da
cui:
da
cui:![]()
Essendo il rapporto di trasmissione
definito da: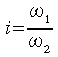 si
otterrà:
si
otterrà: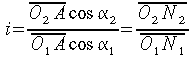
Infine, per similitudine fra i triangoli: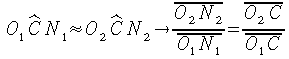 si
ha:
si
ha: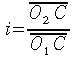
ovvero il rapporto di trasmissione di un ingranaggio cilindrico a denti diritti è pari al rapporto fra i raggi (diametri) delle circonferenze tangenti delle ruote di frizione cilindriche a esse ornologhe, dette circonferenze primitive.
Affinché sia
assicurata la costanza del rapporto di trasmissione durante l'ingranamento
è necessario che la normale di contatto (n n) passi
per il punto C di tangenza di dette circonferenze
(condizione necessaria e sufficiente è la invarianza dei
segmenti ![]() ).Per
questo occorre che i fianchi dei denti siano profilati in maniera opportuna;
ovvero per assicurare la costanza del rapporto di trasmissione e` necessario
che la retta di azione della spinta esercitata dal dente della motrice
sul dente della condotta passi sempre per il punto primitivo C. Praticamente
i profili che consentono questa costanza del rapporto di trasmissione
sono due:
).Per
questo occorre che i fianchi dei denti siano profilati in maniera opportuna;
ovvero per assicurare la costanza del rapporto di trasmissione e` necessario
che la retta di azione della spinta esercitata dal dente della motrice
sul dente della condotta passi sempre per il punto primitivo C. Praticamente
i profili che consentono questa costanza del rapporto di trasmissione
sono due:
-
profilo cicloidale (ordinario, ipocicloidale, epicicloidale): generato da un punto di una circonferenza che rotola, senza strisciare, su una retta o una circonferenza, esternamente o internamente a essa (Figura 2); per la costruzione di ruote dentate tale profilo è stato da tempo abbandonato, salvo qualche applicazione in orologeria e per i compressori/pompe tipo Root, nel caso siano trasmesse ridotte potenze e siano richieste ruote con un ridotto numero di denti; questo perché i denti a profilo cicloidale risultano indeboliti alla base e perché l'angolo di pressione, definito dall'inclinazione della retta di pressione con l'orizzontale (perpendicolare alla congiungente i centri delle ruote coniugate), varia durante l'ingranarnento;
-
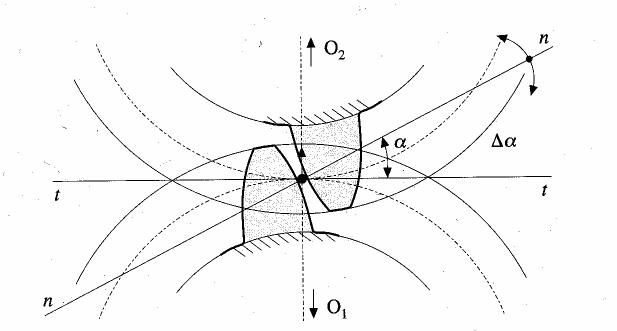
Fig. 5
-
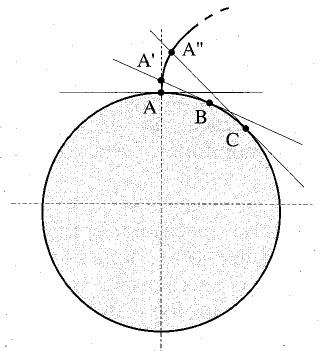
profilo a evolvente di cerchio: ottenuto facendo rotolare senza strisciare una retta su una circonferenza a essa tangente (Figura 3); è impiegato per la costruzione di ingranaggi di potenza in quanto consente di mantenere un rapporto di trasmissione costante nonché assicurare la univocità della retta di pressione, cosicché l'azione di spinta fra i denti si mantiene sempre nella stessa direzione. Per la costruzione grafica dell'evolvente si nota che l'andamento della curva dipende solo esclusivamente dal diametro della circonferenza di riferimento, detta di base; inoltre si ha che le lunghezze dei segmenti
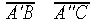 ...
(Figura 3) sono rispettivamente uguali a quelle degli archi AB, AC
...
(Figura 3) sono rispettivamente uguali a quelle degli archi AB, AC
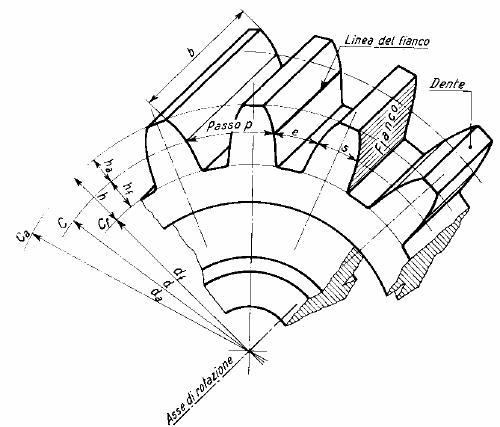
Il proporzionamento di una ruota
dentata, in particolare la sua dentatura, è svolto per convenzione
ed evidente praticità in relazione a una grandezza di riferimento
denominata modulo; si tratta di una grandezza introdotta per agevolare
la costruzione delle ruote dentate, la cui dentatura ha passo: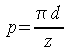
indicando con:
z = numero di denti (numero di vani);
d = diametro primitivo.
il passo di una dentatura,
ovvero la distanza fra due punti omologhi appartenenti a due denti consecutivi
misurata sulla circonferenza primitiva (si tratta di un arco), risulta
di difficile commensurabilità per la presenza, nel membro di destra,
del numero irrazionale p; per questo
si è posto più semplicemente: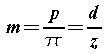
|
|
|
|---|---|
|
Fig. 6 |
Fig. 7 |
a = angolo di pressione formato dalla retta di pressione con la normale alla congiungente i centri di rotazione delle rette costituenti l'ingranaggio (~ 20°);
r = raggio della circonferenza primitiva,, ovvero quello della retta di frizione omologa alla ruota dentata in esame;
rb = r cos a raggio della circonferenza di base o deferente, riferimento per la costruzione del profilo a evolvente dei fianchi dei denti;
N.B. Nel caso i n cui rb > rf i profili dei fianchi dei denti sono prolungati all'interno di rb circa radialmente!!!!
ra = raggio della circonferenza di troncatura esterna, in corrispondenza della quale il profilo ad evolvente viene interrotto
rf = raggio della circonferenza di troncatura interna, in corrispondenza della quale il profilo ad evolvente viene iniziato
ha = addendum, definito come differenza tra il
raggio di troncatura eterna, o raggio di testa, e il raggio primitivo
![]()
hf = dedendum,
definito come differenza fra il raggio primitivo e il raggio di troncatura
interna o di piede: ![]() ;tempo
fa si era soliti porre, anziché hf = 5/ 4 m, assumere
hf = 7/6 m
;tempo
fa si era soliti porre, anziché hf = 5/ 4 m, assumere
hf = 7/6 m
![]() ;
il dedendum e` superiore all'addendum per evitare lo strisciamento della
testa del dente nel vano in cui alloggia
;
il dedendum e` superiore all'addendum per evitare lo strisciamento della
testa del dente nel vano in cui alloggia
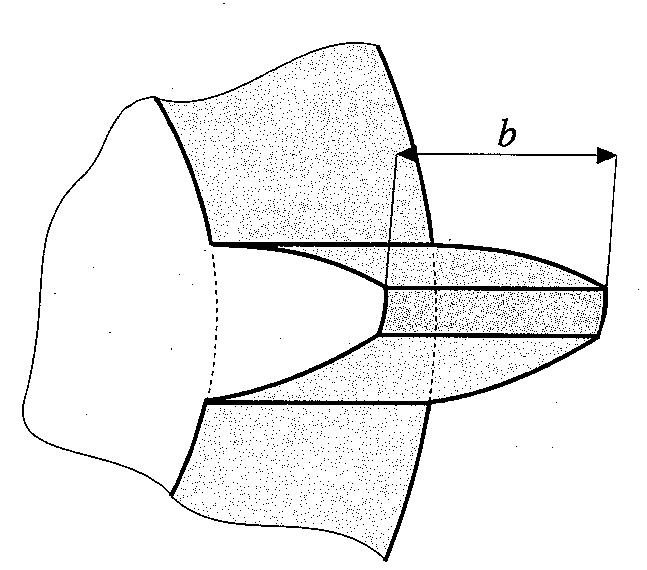
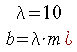 b
= l m (l =
10÷30), passando da ingranaggi ordinari a quelli di precisione)
: larghezza utile della dentatura (fig. 9)
b
= l m (l =
10÷30), passando da ingranaggi ordinari a quelli di precisione)
: larghezza utile della dentatura (fig. 9)
|
|
|
|---|---|
|
Fig. 8 tracciamento dell'evolvente |
Fig. 9 Larghezza della dentatura |
Il profilo geometrico descritto subisce generalmente «ritocchi» per essere più idoneo a un corretto funzionamento/ingranamento:
-
arrotondamento di base = è evitata la realizzazione di spigoli vivi sul fondo del vano, sia per vincoli costruttivi che per rafforzare la base del dente evitando pericolosi effetti d'intaglio; generalmente si assume rf = 0,4 m (Figura 10)
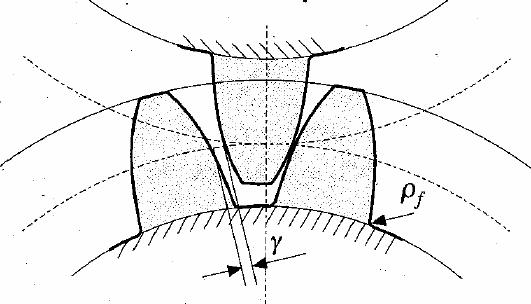
Fig. 10
-
riduzione dello spessore = attuato, se necessario, tra i fianchi oziosi che non prendono parte alla trasmissione, assicurando un opportuno gioco (g) che faciliti la lubrificazione ed eviti impuntamenti (dilatazione termica, variazione dell'interasse...
-
aumento dell'interasse a dentature immutate non rende cinematicamente scorretto il funzionamento della trasmissione, così pure il rapporto di trasmissione, aumentando il dedendum a scapito dell'addendum; di conseguenza si ha un aumento dell'angolo di pressione e maggiori problemi per la resistenza del dente, soggetto a urti all'inversione del senso di marcia, nonché di spessore inferiore.
Affinché sia assicurato l'ingranamento fra due ruote dentate a denti diritti e` necessario che abbiano lo stesso modulo; conseguentemente il relativo rapporto di trasmissione, tenendo presente quanto già esposto anche trattando le ruote di frizione, nonché la definizione di modulo, risulta:
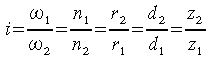
Considerando una coppia di ruote dentate a denti diritti in presa (Figura 11), il contatto fra i relativi fianchi, imposto il senso di rotazione in figura, inizierà in corrispondenza dell'intersezione del cerchio di testa della ruota condotta con la retta di pressione (punto Q1 si svilupperà da detto punto fino a C (fase di «accesso»), proseguirà oltre C (fase di «recesso») per concludersi all'intersezione del cerchio di testa della ruota motrice sempre con la retta di pressione (punto Q2).
Siano le seguenti definizioni geometriche:

condizione necessaria affinché sia assicurata continuità nella trasmissione è che, al cessare del contatto fra una coppia di denti coniugati, sia già iniziata la fase dì condotta relativa alla coppia successiva; il passo della dentatura dovrà essere perciò inferiore all'arco di condotta! Ovvero:
![]()
si
fa sovente riferimento a una grandezza denominata rapporto di condotta:
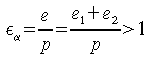
che generalmente è assunto pari a 1,2÷ 2.
Nello studio cinematico dell'ingranamento fra due ruote dentate si è già avuto modo di notare l'esistenza di uno strisciamento relativo fra i fianchi a contatto dei denti in presa. Per avere un'indicazione sull'entità della velocità relativa di strisciamento durante l'ingranamento, all'interno dell'arco di condotta si immagini perciò di rendere immobile la ruota motrice e considerare la ruota condotta rotolante su di essa , attribuendo al sistema una velocità angolare uguale e opposta a w1; ciò significa appunto che la ruota 1 è immobile:
![]()
e che la ruota 2 subisce rotazione attorno al centro d'istantanea rotazione C con velocità angolare:
![]()
Nello spostamento del contatto da Q1 a C (fase di accesso) la velocità di strisciamento con la quale il dente si inserisce nel vano relativo decresce fino ad annullarsi, istantaneamente, nel punto di tangenza dei cerchi primitivi, mentre nella fase di recesso (da C a Q2) riprende ad aumentare; la legge di variazione di tale velocità è di tipo, sostanzialmente, lineare:
![]()
Tali considerazioni sono di fondamentale importanza in quanto gli attriti sviluppati (in relazione al carico sui denti e al loro stato di finitura, nonché al materiale di costruzione) sono causa di usura e riscaldamenti durante il funzionamento, con il pericolo di indurre principi di saldatura sui fianchi dei denti, nonché grippaggi; per evitare simili inconvenienti si adottano oli lubrificanti con particolari additivi, idonei trattamenti superficiali sui denti (per esempio: nitrurazione), oppure, intervenendo direttamente sulla geometria della trasmissione, rendendo minore l'arco di condotta (al fine di ridurre b), conseguenza di un proporzionamento della dentatura con numerosi denti di piccolo modulo.
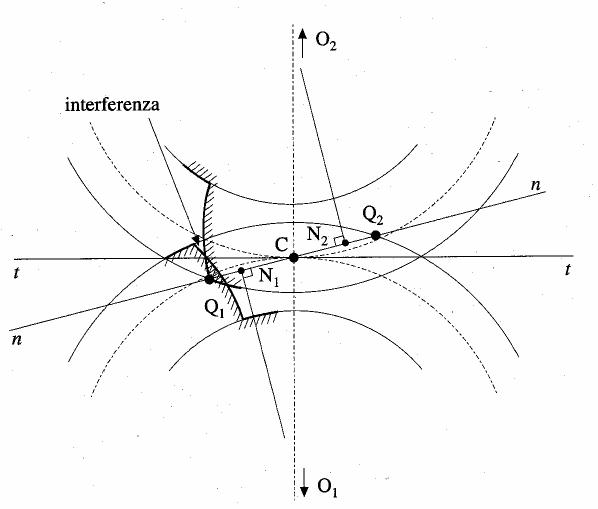
Per
un funzionamento cinematicamente corretto, i cerchi di testa o di troncatura
esterna delle dentature devono intersecare la retta di pressione (punti
Q1, e Q2) internamente al segmento ![]() ,
delimitato dai piedi alla normale di contatto delle perpendicolari a essa
condotte per i centri di rotazione O1 e O2 delle
ruote dentate; è infatti geometricamente dimostrato che, nel caso
ciò non sia verificato (Figura 11), i profili anziché disporsi
tangenti fra loro tendono a compenetrarsi, manifestando interferenza,
sia nella fase di accesso che in quella di recesso. Tale fenomeno, ovviamente
indesiderato in quanto causa di rapido danneggiamento e indebolimento
dei denti della ruota costruita in materiale più tenero, può
poi essere causato anche nella fase di realizzazione della dentatura di
una ruota mediante impiego di una dentiera utensile. In particolari circostanze
si ha che, nel moto di rivoluzione relativo utensile dentiera/ruota,
nel corso del taglio con il procedimento per inviluppo l'utensile realizza
un sensibile e dannoso sottointaglio alla base dei denti.1 suddetti inconvenienti
si hanno fondamentalmente con ruote certamente non proporzionate modularmente,
caratterizzate da denti surdimensionati rispetto aì relativi raggi
primitivi!
,
delimitato dai piedi alla normale di contatto delle perpendicolari a essa
condotte per i centri di rotazione O1 e O2 delle
ruote dentate; è infatti geometricamente dimostrato che, nel caso
ciò non sia verificato (Figura 11), i profili anziché disporsi
tangenti fra loro tendono a compenetrarsi, manifestando interferenza,
sia nella fase di accesso che in quella di recesso. Tale fenomeno, ovviamente
indesiderato in quanto causa di rapido danneggiamento e indebolimento
dei denti della ruota costruita in materiale più tenero, può
poi essere causato anche nella fase di realizzazione della dentatura di
una ruota mediante impiego di una dentiera utensile. In particolari circostanze
si ha che, nel moto di rivoluzione relativo utensile dentiera/ruota,
nel corso del taglio con il procedimento per inviluppo l'utensile realizza
un sensibile e dannoso sottointaglio alla base dei denti.1 suddetti inconvenienti
si hanno fondamentalmente con ruote certamente non proporzionate modularmente,
caratterizzate da denti surdimensionati rispetto aì relativi raggi
primitivi!
|
|
|---|
|
Fig 11 |
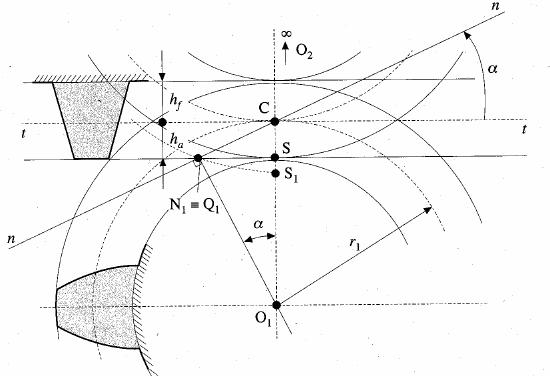
8.2.1. Numero minimo di denti
Le
condizioni geometriche esposte per assicurare un funzionamento cinematicamente
corretto della trasmissione e per evitare interferenze impongono che le
ruote dentate siano realizzate con un sufficiente numero minimo di denti
in relazione al loro diametro primitivo. Consideriamo il caso limite in
cui un pignone o rocchetto ingrana con una dentiera, ovvero una ruota
dentata con raggio primitivo Ñ, i cui
denti sono profilati a trapezio isoscele (evolvente degenere in retta,
segmentata dalle troncature di testa e di base) (Figura 12); in tale accoppiamento
supponiamo, condizione limite ammissibile per evitare interferenza, che![]() (si noti che in questo caso N2 cade all'infinito!), ovvero
il massimo addendum della dentiera sì trova intersecando la retta
di pressione con la retta di testa della dentiera proprio in N1!
In tal caso:
(si noti che in questo caso N2 cade all'infinito!), ovvero
il massimo addendum della dentiera sì trova intersecando la retta
di pressione con la retta di testa della dentiera proprio in N1!
In tal caso:
![]() ma
ma
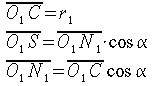
sostituendo:
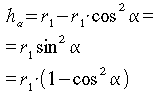
ricordando che:
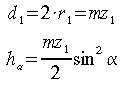
dalla quale il numero (per qualunque tipo di proporzionamento) minimo di denti risulta:
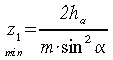
nel caso di proporzionamento modulare: ha = m; ne deriva:
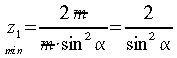
per l'angolo di pressione unificato di 20° si calcola: z1 =. 17
con a= 15° => z1 =30
con a = 22° 30' (dentature rilassate, esempio Fellows) => z1 13
Se si facesse ingranare il pignone, anziché con
la dentiera, con un'altra ruota, si ricaverebbe graficamente un addendum
ha certamente maggiore (![]() ,
di figura 12), in relazione al diametro primitivo di quest'ultima; immutato
il diametro primitivo del pignone, sarebbe possibile diminuire ulteriormente
il numero minimo di denti di questo, rinunciando però al taglio
con utensile dentiera per inviluppo (si avrebbe sotto-intaglio),
ma impiegando particolari frese a profilo costante o sagomate. Si potrebbe
infine pensare di ridurre ulteriormente il numero minimo di denti aumentando
l'angolo di pressione; in tal caso però si ridurrebbe pure il rapporto
di condotta!. Attualmente si utilizza per il calcolo del minimo numero
di denti la seguente relazione:
,
di figura 12), in relazione al diametro primitivo di quest'ultima; immutato
il diametro primitivo del pignone, sarebbe possibile diminuire ulteriormente
il numero minimo di denti di questo, rinunciando però al taglio
con utensile dentiera per inviluppo (si avrebbe sotto-intaglio),
ma impiegando particolari frese a profilo costante o sagomate. Si potrebbe
infine pensare di ridurre ulteriormente il numero minimo di denti aumentando
l'angolo di pressione; in tal caso però si ridurrebbe pure il rapporto
di condotta!. Attualmente si utilizza per il calcolo del minimo numero
di denti la seguente relazione: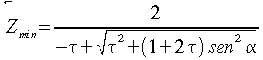
|
|
|---|
|
Fig. 12 |